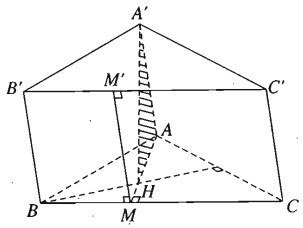
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trực tâm của tam giác ABC và biết rằng A’H vuông góc với mặt phẳng (ABC). Chứng minh rằng:
a) AA ⊥ BC và AA’ ⊥ B’C’.
b) Gọi MM’ là giao tuyến của mặt phẳng (AHA’) với mặt bên BCC’B’, trong đó M ∈ BC và M’ ∈ B’C’. Chứng minh rằng tứ giác BCC’B là hình chữ nhật và MM’ là đường cao của hình chữ nhật đó.

Advertisements (Quảng cáo)
a) \(BC \bot AH\) và \(BC \bot A’H\) vì \(A’H \bot \left( {ABC} \right)\)
\( \Rightarrow BC \bot \left( {A’HA} \right) \Rightarrow BC \bot AA’\)
Và \(B’C’ \bot AA’\) vì \(BC\parallel B’C’\)
b) Ta có \(AA’\parallel BB’\parallel CC’\) mà \(BC \bot AA’\) nên tứ giác BCC’B’ là hình chữ nhật. Vì \(AA’\parallel \left( {BCC’B’} \right)\) nên ta suy ra \(MM’ \bot BC\) và \(MM’ \bot B’C’\) hay MM’ là đường cao của hình chữ nhật BCC’B’.
