Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a. Trên các cạnh bên AA’,BB’,CC’ ta lấy tương ứng các điểm M, N, P sao cho \(AM + BN + CP = a\)
Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.

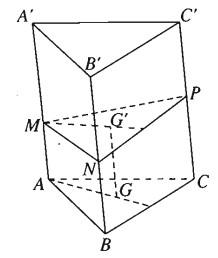
Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và tam giác MNP . Ta có:
\(\eqalign{
& \,\,\,\,\overrightarrow {GG’} = \overrightarrow {GA} + \overrightarrow {AM} + \overrightarrow {MG’} \cr
& + \,\,\overrightarrow {GG’} = \overrightarrow {GB} + \overrightarrow {BN} + \overrightarrow {NG’} \cr
& \,\,\,\,\,\overrightarrow {GG’} = \overrightarrow {GC} + \overrightarrow {CP} + \overrightarrow {PG’} \cr} \)
Advertisements (Quảng cáo)
Cộng từng vế với vế ta có:
\(3\overrightarrow {GG’} = \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} } \right) + \left( {\overrightarrow {MG’} + \overrightarrow {NG’} + \overrightarrow {PG’} } \right)\)
Vì G là trọng tâm của tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) và G’ là trọng tâm của tam giác MNP nên \(\overrightarrow {MG’} + \overrightarrow {NG’} + \overrightarrow {PG’} = \overrightarrow 0 \).
Do đó: \(3\overrightarrow {GG’} = \overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} \)
Hay \(\overrightarrow {GG’} = {1 \over 3}\left( {\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} } \right) = {1 \over 3}\overrightarrow {AA’} \)
Vì điểm G cố định và \({1 \over 3}\overrightarrow {AA’} \) là vectơ không đổi nên G’ là điểm cố định. Vậy mặt phẳng (MNP) luôn luôn đi qua điểm G’ cố định.
