Cho hình hộp ABCD.A’B’C’D’ có P và R lần lượt là trung điểm các cạnh AB và A’D’. Gọi P’, Q, Q’ lần lượt là tâm đối xứng của các hình bình hành ABCD, CDD’C’, A’B’C’D’, ADD’A’
a) Chứng minh rằng \(\overrightarrow {PP’} + \overrightarrow {QQ’} + \overrightarrow {R{\rm{R}}’} = \overrightarrow 0 \)
b) Chứng minh hai tam giác PQRvà P’Q’R’ có trọng tâm trùng nhau.

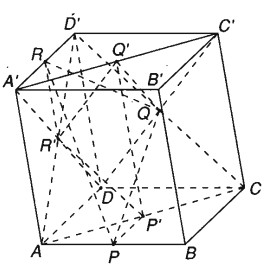
a) Ta có :\(\overrightarrow {PP’} = {1 \over 2}\overrightarrow {A{\rm{D}}} ,\,\,\,\overrightarrow {QQ’} = {1 \over 2}\overrightarrow {DA’} ,\,\,\,\overrightarrow {R{\rm{R}}’} = {1 \over 2}\overrightarrow {A’A} \),
Vậy: \(\overrightarrow {PP’} + \overrightarrow {QQ’} + \overrightarrow {R{\rm{R}}’} = {1 \over 2}\left( {\overrightarrow {A{\rm{D}}} + \overrightarrow {DA} + \overrightarrow {A’A} } \right) = \overrightarrow 0 \)
Advertisements (Quảng cáo)
b) Gọi G và G’ lần lượt là trọng tâm các tam giác PQR và P’Q’R’.
Theo câu a) ta có: \(\overrightarrow {PP’} + \overrightarrow {QQ’} + \overrightarrow {R{\rm{R}}’} = \overrightarrow 0 \)
Do đó:
\(\left( {\overrightarrow {PG} + \overrightarrow {GG’} + \overrightarrow {G’P’} } \right) + \left( {\overrightarrow {QG} + \overrightarrow {GG’} + \overrightarrow {G’Q’} } \right) + \left( {\overrightarrow {RG} + \overrightarrow {GG’} + \overrightarrow {G’R’} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \underbrace {\left( {\overrightarrow {PG} + \overrightarrow {QG} + \overrightarrow {RG} } \right)}_{\overrightarrow 0 } + 3\overrightarrow {GG’} + \underbrace {\left( {\overrightarrow {G’P’} + \overrightarrow {G’Q’} + \overrightarrow {G’R’} } \right)}_{\overrightarrow 0 } = \overrightarrow 0 \)
\(3\overrightarrow {GG’} = \overrightarrow 0 \) ⟹ G trùng với G’
Vậy hai tam giác PQR và P’Q’R’ có cùng trọng tâm.
