Advertisements (Quảng cáo)
Bài 7.32 trang 86 Sách bài tập (SBT) Vật lí 11 nâng cao
Vật sáng AB cách màn ảnh 150 cm. Trong khoảng giữa vật và màn ảnh, ta đặt một thấu kính hội tụ L coi như song song với vật AB. Di chuyển L dọc theo trục chính, ta thấy có hai vị trí của L để ảnh hiện rõ trên màn. Hai vị trí này cách nhau 30 cm.
a) Tìm tiêu cự của L.
b) Tìm số phóng đại của ảnh A’B’ ứng với hai vị trí trên của L.
c) Với thấu kính trên, phải đặt màn ảnh cách vật bao nhiêu thì chỉ có một vị trí của L cho ảnh rõ trên màn ?
a)
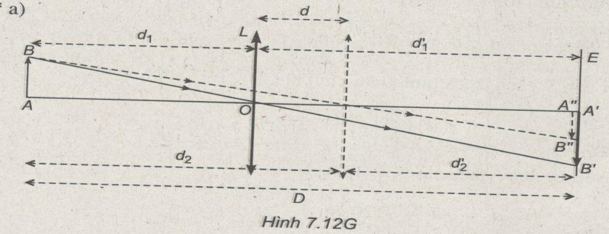
Nhận xét công thức \({1 \over d} + {1 \over {d’}} = {1 \over f}\), ta thấy nếu hoán đổi d thành d’ và d’ thành d thì công thức trở thành \({1 \over {d’}} + {1 \over d} = {1 \over f}\), nghĩa là không có gì thay đổi (so với dạng viết trên).
Như vậy, với vị trí thứ nhất của L, nếu vật cách L là \({d_1}\), ảnh cách L là \(d{‘_1}\) thì với vị trí thứ hai của L, vật cách L là \({d_2} = d{‘_1}\) và ảnh cách L là \(d{‘_2} = {d_1}\) (Hình 7.12G).
Vậy ta có hệ phương trình sau :
\(\eqalign{
& {d_1} + d{‘_1} = D \cr
& d{‘_1} – {d_1} = d \cr} \)
Suy ra : \(d{‘_1} = {{D + d} \over 2},{d_1} = {{D – d} \over 2}\)
Vậy : \({1 \over f} = {1 \over {{d_1}}} + {1 \over {d{‘_1}}} = {2 \over {D – d}} + {2 \over {D + d}} = {{4D} \over {{D^2} – {d^2}}}\)
\( \Rightarrow \) Tiêu cự thấu kính :
\(f = {{{D^2} – {d^2}} \over {4D}}\) với \(D = 15cm,d = 30cm\)
Advertisements (Quảng cáo)
\(f = 36cm\)
b) Số phóng đại :
– Khi L ở vị trí thứ nhất :
\({k_1} = – {{d{‘_1}} \over {{d_1}}}\) với \(d{‘_1} = {{D + d} \over 2} = 90cm,{d_1} = {{D – d} \over 2} = 60cm\)
\({k_1} = – {3 \over 2}\)
– Khi L ở trị trí thứ hai :
\({k_2} = – {{d{‘_2}} \over {{d_2}}} = – {{{d_1}} \over {d{‘_1}}} = – {2 \over 3}\).
c) Từ công thức trên của f, ta suy ra :
\({d^2} = {D^2} – 4Df = D\left( {D – 4f} \right)\)
Vì \({d^2} > 0\), suy ra điều kiện \(D > 4f\).
Vậy, muốn thí nghiệm xảy ra như trên, khoảng cách D giữa vật AB và màn E phải thỏa mãn điều kiện \(D > 4f\).
Ta chỉ có một vị trí của L cho ảnh rõ trên màn khi \(D = 4f\). Khi đó d = 0; nghĩa là hai vị trí của L trở thành trùng nhau.
\(D = 4f = 144cm\).