Hoạt động6

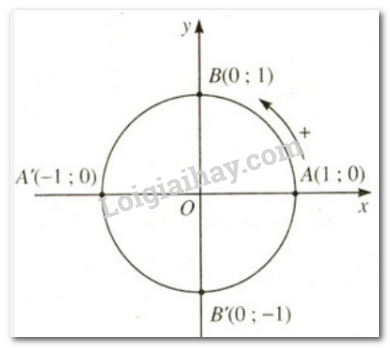
a) Trong mặt phẳng tọa độ (định hướng) Oxy, hãy vẽ đường tròn tâm O và bán kính bằng 1

b) Hãy nêu chiều dương, chiều âm trên đường tròn tâm O với bán kính bằng 1

Dựa vào kiến thực đã học về trục tọa độ và kiến thức học ở phần trên để xác vẽ hình

a) b)

Luyện tập-VD6

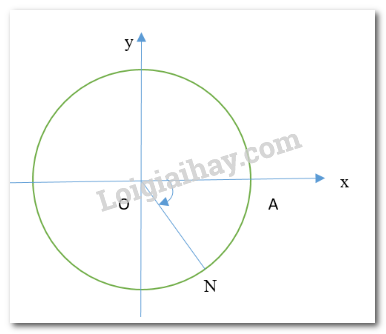
Xác định điểm N trên đường tròn lượng giác sao cho \(\left( {OA,ON} \right) = - \frac{\pi }{3}\)

Dựa vào kiến thực đã học về trục tọa độ và kiến thức học ở phần trên để xác vẽ

Hoạt động7

a) Xác định điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = 60^\circ \)

b) So sánh hoành độ của điểm M với \(\cos 60^\circ \); tung độ của điểm M với \(\sin 60^\circ \)

Dựa vào cách xác định góc bên trên để xác định

a)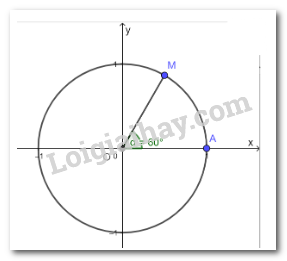

b) \(\cos 60^\circ \) bằng hoành độ của điểm M

\(\sin 60^\circ \) bằng tung độ của điểm M

Luyện tập-VD7

Tìm giác trị lượng giác của góc lượng giác \(\beta = - \frac{\pi }{4}\)

Dựa vào kiến thức đã học để tính

\(\sin \left( { - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2};\,\,\cos \left( { - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( { - \frac{\pi }{4}} \right) = - \frac{1}{2};\,\,\cot \left( { - \frac{\pi }{4}} \right) = - 2\)

Hoạt động8

Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \)

Dựa vào sin, cos, tan, cot đã học ở lớp dưới để xác định

\(\begin{array}{l}\cos \left( { - 30^\circ } \right) = \frac{{\sqrt 3 }}{2} > 0\\\sin \left( { - 30^\circ } \right) = - \frac{1}{2} < 0\\\tan \left( { - 30^\circ } \right) = - \frac{{\sqrt 3 }}{3} < 0\\\cot \left( { - 30^\circ } \right) = - \sqrt 3 < 0\end{array}\)

Luyện tập-VD8

Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\)

Dựa vào bảng xét dấu sau:

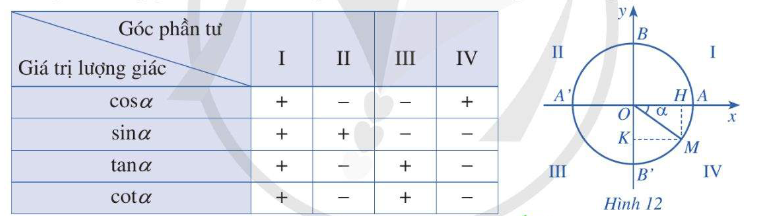
Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên

\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\)

Hoạt động9

Cho góc lượng giác \(\alpha \). So sánh

a) \({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\) và 1

b) \(\tan \alpha .\cot \alpha \,\,\) và 1 với \(\cos \alpha \ne 0;\sin \alpha \ne 0\)

c) \(1 + {\tan ^2}\alpha \,\,\) và \(\frac{1}{{{{\cos }^2}\alpha }}\) với \(\cos \alpha \ne 0\)

d) \(1 + {\cot ^2}\alpha \,\) và \(\frac{1}{{{{\sin }^2}\alpha }}\) với \(\sin \alpha \ne 0\)

Dựa vào kiến thức của phần phía trên và kiến thức lớp 9 để so sánh

a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)

b) \(\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\)

c) \(\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\)

d) \(\frac{1}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha \)

Luyện tập-VD9

Cho góc lượng giác \(\alpha \)sao cho \(\pi < \alpha < \frac{{3\pi }}{2}\) và \(\sin \alpha = - \frac{4}{5}\). Tìm \(\cos \alpha \)

Sử dụng công thức lượng giác \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)

Vì \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\) nên \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{4}{5}} \right)^2} = \frac{9}{{25}}\)

Do \(\pi < \alpha < \frac{{3\pi }}{2}\) nên \(\cos \alpha < 0\). Suy ra \(\cos \alpha = - \frac{3}{5}\)

Hoạt động10

Tìm các giá trị lượng giác của góc lượng giác \(\alpha = 45^\circ \)

Dựa vào các kiến thức đã học để tính

\(\sin \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\cos \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( {45^\circ } \right) = \frac{1}{2};\,\,\cot \left( {45^\circ } \right) = 2\)

Luyện tập-VD10

Tính giá trị của biểu thức:

\(Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\)

Sử dựng bảng lượng giác của các góc đặc biệt

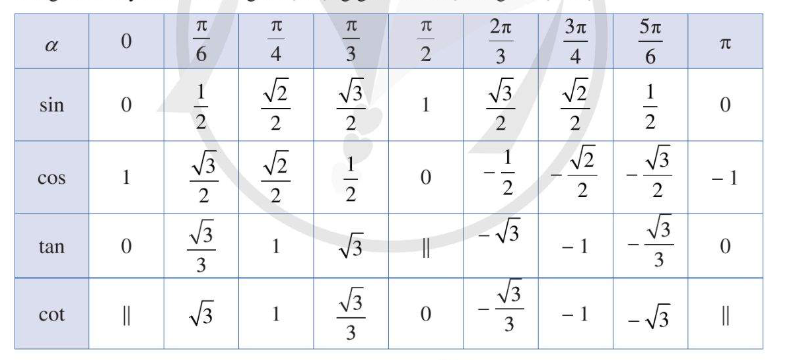
Ta có

\(\begin{array}{l}Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\\\,\,\,\,\, = \,{\left( {\sqrt 3 } \right)^2} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + 1 + 0 = \frac{7}{2}\end{array}\)

Hoạt động11

Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha ,\,\,\left( {OA,OM’} \right) = - \alpha \) (Hình 13)

a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.

b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \) và \(- \alpha \)

Dựa vào hình vẽ ( hình 13)

a) Hoành độ của điểm M và M’ bằng nhau

Tung độ của điểm M và M’ đối nhau

b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha\) và \(- \alpha \)

Luyện tập-VD11

a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8}\)

b) \(\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\)

Sử dụng công thức trong bảng:

a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} = {\cos ^2}\frac{\pi }{8} + {\cos ^2}\left( {\frac{\pi }{2} - \frac{\pi }{8}} \right) = {\cos ^2}\frac{\pi }{8} + {\sin ^2}\frac{\pi }{8} = 1\)

b)

\(\begin{array}{l}\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\\ = (\tan {1^ \circ }.\tan {89^ \circ }).(\tan {2^ \circ }.\tan {88^ \circ }).\tan {45^ \circ }\\ = (\tan {1^ \circ }.\cot {1^ \circ }).(\tan {2^ \circ }.\cot {2^ \circ }).\tan {45^ \circ }\\ = 1\end{array}\)

Luyện tập-VD12

Dùng máy tính cầm tay để tính ;

a) \(\tan ( - {75^ \circ });\)b) \(\cot \left( { - \frac{\pi }{5}} \right)\)

Sử dụng máy tính cầm tay

a) \(\tan ( - {75^ \circ }) = - 2 - \sqrt 3 \)

b) \(\cot \left( { - \frac{\pi }{5}} \right) \approx - 1,376\)