I. Góc lượng giác
1. Góc hình học và số đo của chúng
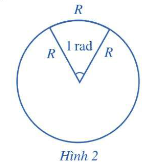
*Nhận xét:
- Đơn vị đo góc: độ hoặc radian (rad).
- Ta có: \({180^o} = \pi \)rad, do đó 1 rad \( = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \left( {\frac{\pi }{{180}}} \right)\)rad.
- Người ta thường không viết chữ radian hay rad sau số đo góc.
VD: \(\frac{\pi }{2}\)rad cũng được viết là \(\frac{\pi }{2}\).
2. Góc lượng giác và số đo của chúng
a, Khái niệm
- Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
- Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.
b, Tính chất
- Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau \(\left( {Ou \equiv O’u’} \right)\), tia cuối trùng nhau \(\left( {Ov \equiv O’v’} \right)\).
Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:
\(\left( {Ou,Ov} \right) = \left( {O’u’,O’v’} \right) + k{360^o},k \in \mathbb{Z}.\)
Nếu sử dụng đơn vị đo là radian thì:
\(\left( {Ou,Ov} \right) = \left( {O’u’,O’v’} \right) + k2\pi ,k \in \mathbb{Z}.\)
* Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
(Ou,Ov) + (Ov, Ow) = (Ou,Ow) \( + k2\pi ,k \in \mathbb{Z}.\)
II. Giá trị lượng giác của góc lượng giác
1. Đường tròn lượng giác
Advertisements (Quảng cáo)
Trong mặt phẳng toa độ đã được định hướng Oxy, lấy điểm A(1;0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.
2. Giá trị lượng giác của góc lượng giác
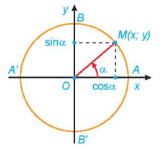
- Trục tung là trục sin, trục hoành là trục côsin.
- Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)
* Dấu của các giá trị lượng giác của góc \(\alpha \)
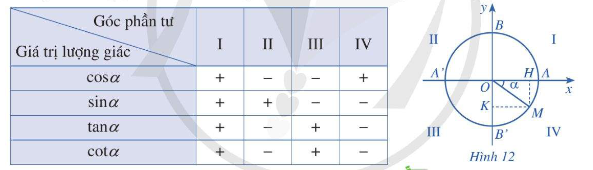
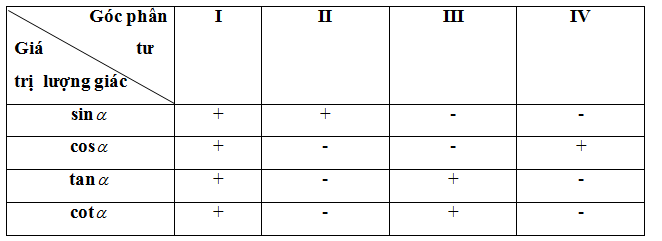
* Các công thức lượng giác cơ bản
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
3. Giá trị lượng giác của các góc có liên quan đặc biệt
- Hai góc đối nhau \(\alpha \) và \( - \alpha \)
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc bù nhau (\(\alpha \) và \(\pi \)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc phụ nhau (\(\alpha \) và \(\frac{\pi }{2}\)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
- Hai góc hơn kém \(\pi \)(\(\alpha \) và \(\pi \) + \(\alpha \))
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
4. Sử dụng máy tính cầm tay để tính giá trị của một góc lượng giác
Đơn vị độ:

Đơn vị radian:


