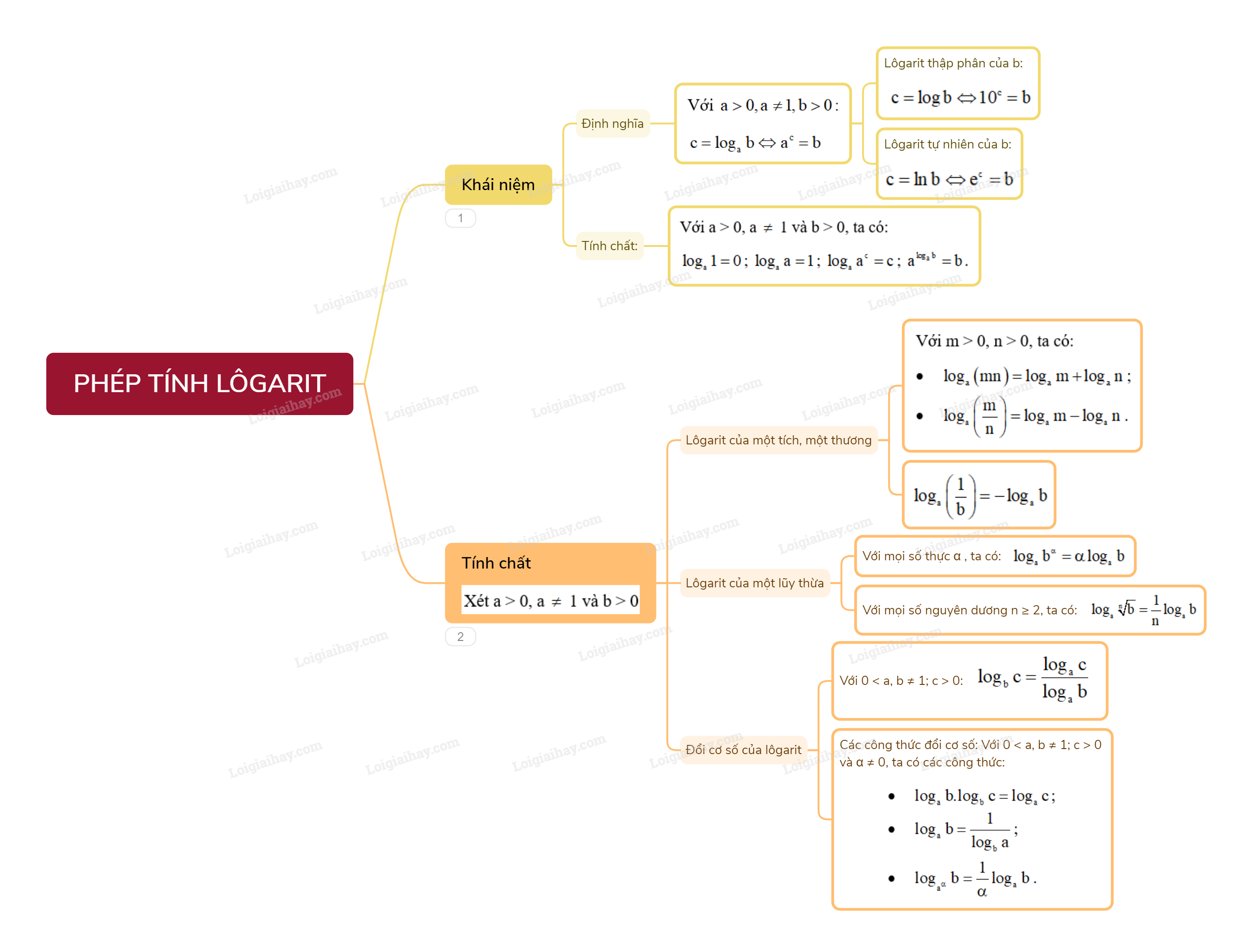
1. Khái niệm lôgarit
a) Định nghĩa
Với a > 0, a \( \ne \) 1 và b > 0, ta có: \(c = {\log _a}b \Leftrightarrow {a^c} = b\). Ngoài ra:
- Lôgarit thập phân của b là lôgarit cơ số 10 của số thực dương b:
\(c = \log b \Leftrightarrow {10^c} = b\)
- Lôgarit tự nhiên của b là lôgarit cơ số e của số thực dương b:
\(c = \ln b \Leftrightarrow {e^c} = b\).
b) Tính chất
Với a > 0, a \( \ne \) 1 và b > 0, ta có:
\({\log _a}1 = 0\); \({\log _a}a = 1\); \({\log _a}{a^c} = c\); \({a^{{{\log }_a}b}} = b\).
2. Một số tính chất của phép tính lôgarit
Advertisements (Quảng cáo)
Trong mục này, ta xét a > 0, a \( \ne \) 1 và b > 0.
a) Lôgarit của một tích, một thương
Với m > 0, n > 0, ta có:
- \({\log _a}\left( {mn} \right) = {\log _a}m + {\log _a}n\);
- \({\log _a}\left( {\frac{m}{n}} \right) = {\log _a}m - {\log _a}n\).
Nhận xét: \({\log _a}\left( {\frac{1}{b}} \right) = - {\log _a}b\).
b) Lôgarit của một lũy thừa
Với mọi số thực \(\alpha \), ta có: \({\log _a}{b^\alpha } = \alpha {\log _a}b\).
Nhận xét: Với mọi số nguyên dương \(n \ge 2\), ta có: \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\).
c) Đổi cơ số của lôgarit
Với a, b là hai số thực dương khác 1 và c là số thực dương, ta có: \({\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}\).
Nhận xét: Với a, b là hai số thực dương khác 1, c > 0 và \(\alpha \ne 0\), ta có những công thức sau:
- \({\log _a}b.{\log _b}c = {\log _a}c\);
- \({\log _a}b = \frac{1}{{{{\log }_b}a}}\);
- \({\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b\).