
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(C\), mặt bên \(SAC\) là tam giác đều và nằm trong mặt phẳng vuông góc với \(\left( {ABC} \right)\).
a) Chứng minh rằng \(\left( {SBC} \right) \bot \left( {SAC} \right)\).
b) Gọi \(I\) là trung điểm của \(SC\). Chứng minh rằng \(\left( {ABI} \right) \bot \left( {SBC} \right)\).

Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.

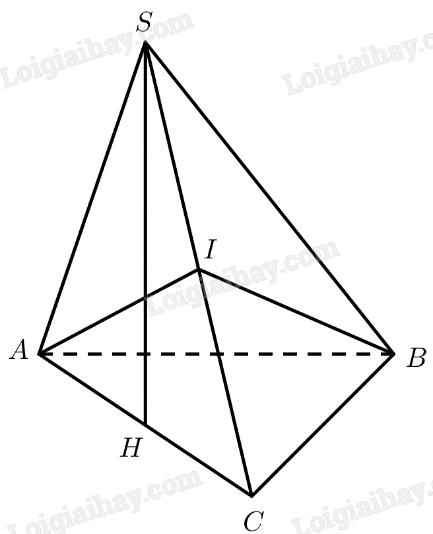
a) Gọi \(H\) là trung điểm của \(AC\)
Advertisements (Quảng cáo)
\(SAC\) là tam giác đều \( \Rightarrow SH \bot AC\)
Mà \(\left( {SAC} \right) \bot \left( {ABC} \right)\)
\( \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot BC\)
Lại có \(AC \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SAC} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SAC} \right)\)
b) \(SAC\) là tam giác đều \( \Rightarrow AI \bot SC\)
\(BC \bot \left( {SAC} \right) \Rightarrow BC \bot AI\)
\(\left. \begin{array}{l} \Rightarrow AI \bot \left( {SBC} \right)\\AI \subset \left( {ABI} \right)\end{array} \right\} \Rightarrow \left( {ABI} \right) \bot \left( {SBC} \right)\)
