
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).

Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.

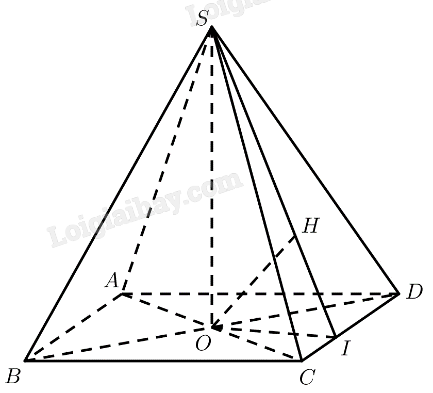
Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
Advertisements (Quảng cáo)
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).
