
Cho mặt phẳng \(\left( \alpha \right)\) và hai đường thẳng chéo nhau \(a,b\) cắt \(\left( \alpha \right)\) tại \(A\) và \(B\). Gọi \(d\) là đường thẳng thay đổi luôn luôn song song với \(\left( \alpha \right)\) và cắt \(a\) tại \(M\), cắt \(b\) tại \(N\). Qua điểm \(N\) dựng đường thẳng song song với \(a\) cắt \(\left( \alpha \right)\) tại điểm \(C\).
a) Tứ giác \(MNCA\) là hình gì?
b) Chứng minh rằng điểm \(C\) luôn luôn chạy trên một đường thẳng cố định.
c) Xác định vị trí của đường thẳng \(d\) để độ dài \(MN\) nhỏ nhất.

Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

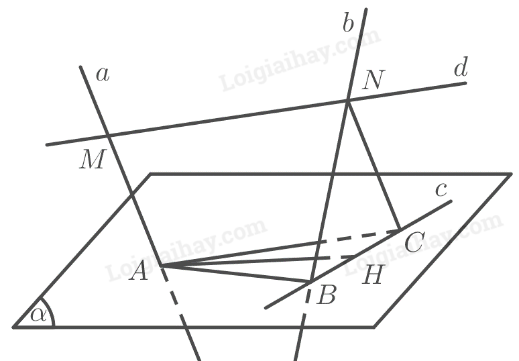
a) Ta có:
\(\left. \begin{array}{l}d \subset \left( {AMNC} \right)\\d\parallel \left( \alpha \right)\\\left( \alpha \right) \cap \left( {AMNC} \right) = AC\end{array} \right\} \Rightarrow d\parallel AC \Rightarrow MN\parallel AC\)
Mà \(a\parallel NC \Rightarrow MA\parallel NC\)
Advertisements (Quảng cáo)
\( \Rightarrow AMNC\) là hình bình hành.
b) Gọi \(\left( \beta \right)\) là mặt phẳng chứa \(b\) và song song với \(a\), \(c = \left( \alpha \right) \cap \left( \beta \right)\)
Ta có:
\(\left. \begin{array}{l}NC\parallel a\\N \in b\end{array} \right\} \Rightarrow NC \subset \left( \beta \right)\)
\( \Rightarrow C \in \left( \alpha \right) \cap \left( \beta \right) \Rightarrow C \in c\)
Vậy điểm \(C\) luôn luôn chạy trên đường thẳng \(c\) là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) cố định.
c) Trong mặt phẳng \(\left( \alpha \right)\), kẻ \(AH \bot c\)
Vì \(c\) cố định nên \(AC \ge AH\)
\(AMNC\) là hình bình hành \( \Rightarrow MN = AC\)
Vậy \(MN \ge AH\)
Vậy \(MN\) nhỏ nhất khi \(C \equiv H\). Khi đó \(d\parallel AH\).
