
Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng khác nhau. Lấy các điểm \(M,N\) lần lượt thuộc các đường chéo \(AC\) và \(BF\) sao cho \(MC = 2MA;NF = 2NB\). Qua \(M,N\) kẻ các đường thẳng song song với \(AB\), cắt các cạnh \(AD,AF\) lần lượt tại \({M_1},{N_1}\). Chứng minh rằng:
a) \(MN\parallel DE\);
b) \({M_1}{N_1}\parallel \left( {DEF} \right)\);
c) \(\left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\).

Sử dụng các định lí, tính chất:
‒ Tính chất trọng tâm của tam giác.
‒ Định lí Thalès trong tam giác.
– Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).
‒ Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\).

Advertisements (Quảng cáo)
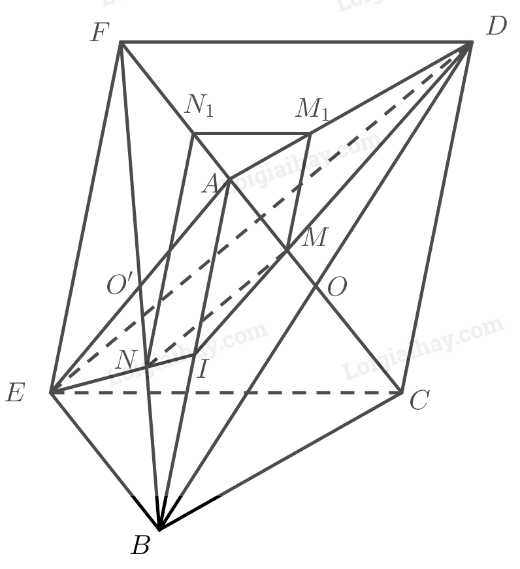
+) Trong mặt phẳng (ABCD) kéo dài DM cắt AB tại O
Vì AO // DC nên \(\frac{{AO}}{{DC}} = \frac{{AM}}{{MC}} = \frac{{OM}}{{MD}} = \frac{1}{2}\) (định lí Thales)
Suy ra AO=1/2AB =>\(AO = \frac{1}{2}AB\)
+) Gọi N’ là giao điểm của BF và OE, khi đó: \(\frac{{OB}}{{FE}} = \frac{{BN’}}{{N’F}} = \frac{{ON’}}{{N’F}} = \frac{1}{2} \Rightarrow BN’ = 2N’F\) nên N’ trùng N
+) Trong mặt phẳng (ODE), có: \(\frac{{OM}}{{DM}} = \frac{{ON}}{{NE}} = \frac{1}{2}\).
Suy ra MN // DE (định lí Thales đảo).
b) Ta có: MM1 // AB // DC nên \(\frac{{A{M_1}}}{{D{M_1}}} = \frac{{AM}}{{MC}} = \frac{1}{2}\).
Ta lại có: NN1 // AB // EF nên \(\frac{{A{N_1}}}{{{N_1}F}} = \frac{{BN}}{{BF}} = \frac{1}{2}\)
Suy ra \(\frac{{A{M_1}}}{{D{M_1}}} = \frac{{A{N_1}}}{{{N_1}F}} = \frac{1}{2}\)Do đó M1N1 // DF
Mà DF ⊂ (DEF) nên M1N1 // (DEF).
c) Ta có: MN // DE, M1N1 // DF mà DE, DF ⊂ (DEF) và MN, M1N1 ⊂ (MNN1M1); DE và DF cắt nhau tại E nên (MNN1M1) // (DEF).
