
Cho hình vuông \(ABCD\). Gọi \(H,K\) lần lượt là trung điểm của \(AB,AD\). Trên đường thẳng vuông góc với \(\left( {ABCD} \right)\) tại \(H\), lấy điểm \(S\). Chứng minh rằng:
a) \(AC \bot \left( {SHK} \right)\);
b) \(CK \bot \left( {SDH} \right)\).

Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

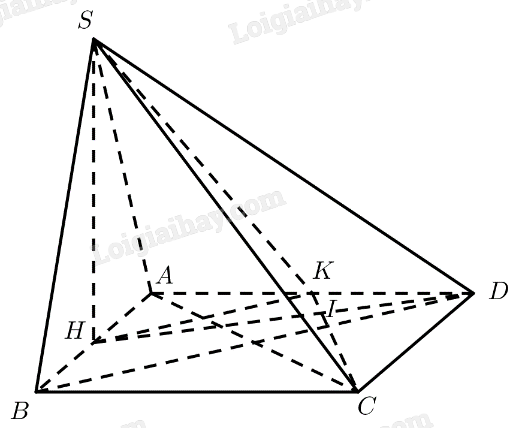
a) Ta có:
\(H\) là trung điểm của \(AB\)
\(K\) là trung điểm của \(AD\)
Advertisements (Quảng cáo)
\( \Rightarrow HK\) là đường trung bình của \(\Delta ABD\)
\( \Rightarrow HK\parallel B{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
Ta có: \(\left\{ \begin{array}{l}AC \bot BD\\HK//BD\end{array} \right. \Rightarrow AC \bot HK\)
Ta có: \(\left\{ \begin{array}{l}AC \bot HK - cmt\\AC \bot SH\,(Do\,SH \bot (ABCD))\\HK,SH \subset (SHK);HK \cap SH\end{array} \right. \Rightarrow AC \bot (SHK)\)
b) Gọi \(I = CK \cap DH\).
Xét \(\Delta AH{\rm{D}}\) và \(\Delta DKC\) có:
\(\left. \begin{array}{l}AH = DK\\\widehat {HA{\rm{D}}} = \widehat {K{\rm{D}}C}\\A{\rm{D}} = C{\rm{D}}\end{array} \right\} \Rightarrow \Delta AH{\rm{D}} = \Delta DKC\left( {c.g.c} \right) \Rightarrow \widehat {A{\rm{D}}H} = \widehat {DCK}\)
Mà \(\widehat {DKC} + \widehat {DCK} = {90^ \circ }\)
\(\begin{array}{l} \Rightarrow \widehat {DKC} + \widehat {ADH} = {90^0} \Rightarrow \widehat {DKI} = {180^0} - (\widehat {DKC} + \widehat {ADH}) = {90^0}\\ \Rightarrow DH \bot CK\end{array}\)
Ta có: \(\left\{ \begin{array}{l}CK \bot DH - cmt\\CK \bot SH\,\,(Do\,SH \bot (ABCD))\\DH,SH \subset (SDH);DH \cap SH\end{array} \right. \Rightarrow CK \bot (SDH)\)
