
Cho tam giác đều \(ABC\) cạnh \(a\), \(I\) là trung điểm của \(BC\), \(D\) là điểm đối xứng với \(A\) qua \(I\). Vẽ đoạn thẳng \(S{\rm{D}}\) có độ dài bằng \(\frac{{a\sqrt 6 }}{2}\) và vuông góc với \(\left( {ABC} \right)\). Chứng minh rằng:
a) \(\left( {SBC} \right) \bot \left( {SAD} \right)\);
b) \(\left( {SAB} \right) \bot \left( {SAC} \right)\).

Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.

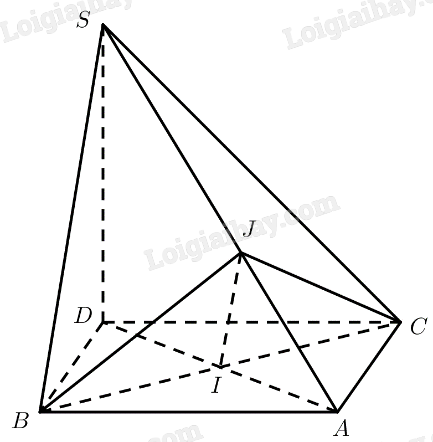
a) \(ABC{\rm{D}}\) là hình thoi \( \Rightarrow A{\rm{D}} \bot BC\)
\(S{\rm{D}} \bot \left( {ABC} \right) \Rightarrow S{\rm{D}} \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SA{\rm{D}}} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
b) Kẻ \(IJ \bot SA\left( {J \in SA} \right)\).
Advertisements (Quảng cáo)
\(\Delta ABC\) đều \( \Rightarrow AI = \frac{{a\sqrt 3 }}{2} \Rightarrow A{\rm{D}} = 2AI = a\sqrt 3 \)
\(\Delta SAD\) vuông tại \(D\) \( \Rightarrow S{\rm{A}} = \sqrt {S{D^2} + A{{\rm{D}}^2}} = \frac{{3a\sqrt 2 }}{2}\)
Xét \(\Delta SAD\) và \(\Delta IAJ\)có:
\(\begin{array}{l}\widehat {SDA} = \widehat {IJA} = {90^0}\\\widehat A\,\,chung\end{array}\)
Suy ra \(\Delta SAD\,\infty \,\Delta IAJ\,(g.g) \Rightarrow \frac{{JI}}{{SD}} = \frac{{AI}}{{SA}} \Rightarrow JI = \frac{{SD.AI}}{{SA}} = \frac{{\frac{{a\sqrt 6 }}{2}.\frac{{a\sqrt 3 }}{2}}}{{\frac{{3a\sqrt 2 }}{2}}} = \frac{a}{2}\)
Nên \(JI = \frac{{BC}}{2}\)
Tam giác \(BCJ\) có \(IJ\) là trung tuyến và \(IJ = \frac{1}{2}BC\)
Vậy tam giác \(BCJ\) vuông tại \(J \Rightarrow BJ \bot JC\)
\(\begin{array}{l}\left. \begin{array}{l}BC \bot \left( {SA{\rm{D}}} \right) \Rightarrow BC \bot SA\\IJ \bot SA\end{array} \right\} \Rightarrow SA \bot \left( {BCJ} \right)\\\left. \begin{array}{l} \Rightarrow SA \bot BJ\\BJ \bot JC\end{array} \right\} \Rightarrow BJ \bot \left( {SAC} \right)\end{array}\)
Mà \(BJ \subset \left( {SAB} \right)\)
Vậy \(\left( {SAB} \right) \bot \left( {SAC} \right)\).
