
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {BSA} = \widehat {CSA} = {60^ \circ },\) \(\widehat {BSC} = {90^ \circ }\). Cho \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(BC\). Chứng minh rằng \(IJ \bot SA\) và \(IJ \bot BC\).

Để chứng minh hai đường thẳng vuông góc, ta chứng minh góc giữa chúng bằng \({90^ \circ }\).

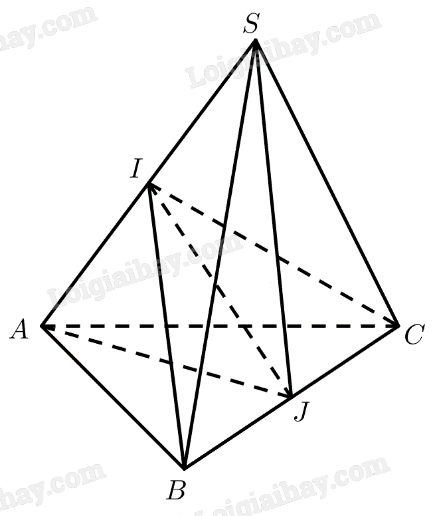
Xét tam giác SAB có:
SA = SB = a
\(\widehat {BSA} = {60^0}\)
⇒ Tam giác SAB đều.
Mà I là trung điểm của SA ⇒ \(IB = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác SAC có:
SA = SC = a
\(\widehat {ASC} = {60^0}\)
⇒ Tam giác SAC đều.
Mà I là trung điểm của SA ⇒ \(IC = \frac{{a\sqrt 3 }}{2}\)
Ta có BSC là tam giác vuông cân tại S.
⇒ BC=\(\sqrt {S{B^2} + S{C^2}} = a\sqrt 2 \)
Xét tam giác ABC:
Advertisements (Quảng cáo)
AB = AC = a
\(\begin{array}{l}A{B^2} + A{C^2} = {a^2} + {a^2} = 2{a^2}\\B{C^2} = {\left( {a\sqrt 2 } \right)^2} = 2{a^2}\\ \Rightarrow A{B^2} + A{C^2} = B{C^2}\end{array}\)
⇒ Tam giác ABC vuông cân tại A.
Mà J là trung điểm đoạn BC ⇒ AJ \( \bot \) BC
⇒ \(AJ = \sqrt {A{B^2} - B{J^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác SBC vuông cân tại S:
Mà J là trung điểm đoạn BC ⇒ SJ \( \bot \) BC
⇒ \(SJ = \sqrt {S{B^2} - B{J^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác JSA:
AJ = SJ = \(\frac{{a\sqrt 2 }}{2}\)
⇒ Tam giác JSA cân tại J.
Mà I là trung điểm của SA ⇒ IJ là đường trung tuyến của tam giác JSA.
hay IJ ⊥SA.
Xét tam giác IBC:
IB = IC =\(\frac{{a\sqrt 3 }}{2}\)
⇒ Tam giác IBC cân tại I.
Mà J là trung điểm của BC ⇒ IJ là đường trung tuyến của tam giác IBC.
hay IJ \( \bot \) BC.
