
Cho hình hộp \(ABCD.A’B’C’D’\). Gọi \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác \(BDA’\) và \(B’D’C\). Chứng minh \({G_1}\) và \({G_2}\) chia đoạn \(AC\) thành ba phần bằng nhau.

‒ Sử dụng tính chất hình hộp.
‒ Sử dụng tính chất trọng tâm của tam giác.

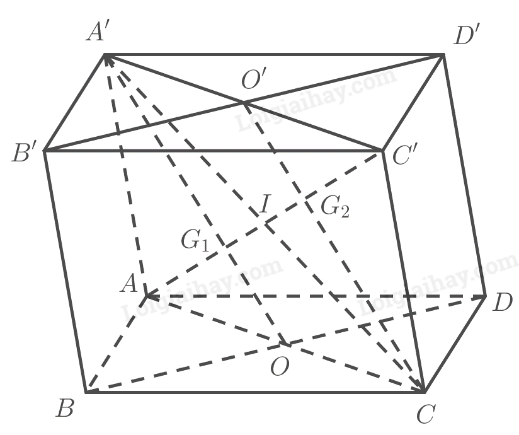
Gọi \(O = AC \cap B{\rm{D}},O’ = A’C’ \cap B'{\rm{D}}’,I = AC’ \cap A’C\)
Vì \(AA’\parallel CC’,AA’ = CC’\) theo tính chất hình hộp nên \(AA’C’C\) là hình bình hành \( \Rightarrow I\) là trung điểm của \(AC’\) và \(A’C\).
Ta có: \({G_1}\) là trọng tâm của tam giác \(BDA’ \Rightarrow \frac{{A'{G_1}}}{{A’O}} = \frac{2}{3}\)
Advertisements (Quảng cáo)
Tam giác \(AA’C\) có \(\frac{{A'{G_1}}}{{A’O}} = \frac{2}{3}\) nên \({G_1}\) là trọng tâm của tam giác \(AA’C\)
Mà \(I\) là trung điểm của \(A’C\) nên \(\frac{{A{G_1}}}{{AI}} = \frac{2}{3} \Rightarrow A{G_1} = \frac{2}{3}AI\)
Mà \(AI = \frac{1}{2}AC’\)
\( \Rightarrow A{G_1} = \frac{1}{3}AC’\left( 1 \right)\)
Ta có: \({G_2}\) là trọng tâm của tam giác \(B’D’C \Rightarrow \frac{{C{G_2}}}{{CO’}} = \frac{2}{3}\)
Tam giác \(ACC’\) có \(\frac{{C{G_2}}}{{CO’}} = \frac{2}{3}\) nên \({G_2}\) là trọng tâm của tam giác \(ACC’\)
Mà \(I\) là trung điểm của \(AC’\) nên \(\frac{{C'{G_2}}}{{C’I}} = \frac{2}{3} \Rightarrow C'{G_2} = \frac{2}{3}C’I\)
Mà \(C’I = \frac{1}{2}AC’\)
\( \Rightarrow C'{G_2} = \frac{1}{3}AC’\left( 2 \right)\)
Từ (1) và (2) suy ra \({G_1}\) và \({G_2}\) chia đoạn \(AC\) thành ba phần bằng nhau.
