Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(BC\) và \(A{\rm{D}}\). Biết \(AB = CD = 2a\) và \(MN = a\sqrt 3 \). Tính góc giữa \(AB\) và \(C{\rm{D}}\).
Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a’\parallel a\) và đường thẳng \(b’\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a’,b’} \right)\).
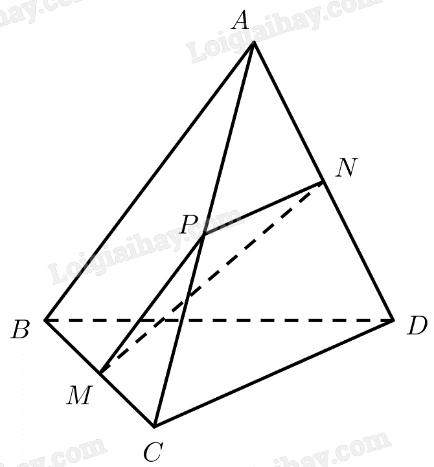
Gọi \(P\) là trung điểm của \(AC\).
Ta có: \(M\) là trung điểm của \(BC\)
\(P\) là trung điểm của \(AC\)
\( \Rightarrow MP\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MP\parallel AB,MP = \frac{1}{2}AB = a\)
\(N\) là trung điểm của \(A{\rm{D}}\)
\(P\) là trung điểm của \(AC\)
\( \Rightarrow NP\) là đường trung bình của tam giác \(AC{\rm{D}}\)
\( \Rightarrow NP\parallel C{\rm{D}},NP = \frac{1}{2}C{\rm{D}} = a\)
Ta có: \(MP\parallel AB,NP\parallel C{\rm{D}} \Rightarrow \left( {AB,C{\rm{D}}} \right) = \left( {MP,NP} \right)\)
Xét tam giác \(MNP\) có:
\(\cos \widehat {MPN} = \frac{{M{P^2} + N{P^2} - M{N^2}}}{{2.MP.NP}} = - \frac{1}{2} \Rightarrow \widehat {MPN} = {120^ \circ }\)
Vậy \(\left( {AB,C{\rm{D}}} \right) = {180^ \circ } - \widehat {MPN} = {60^ \circ }\).