
Cho hình chóp tam giác đều \(S.ABC\) cạnh đáy bằng \(2a\) và chiều cao bằng \(a\sqrt 2 \). Khoảng cách từ tâm \(O\) của đáy \(ABC\) đến một mặt bên là
A. \(\frac{{a\sqrt {14} }}{7}\).
B. \(\frac{{a\sqrt 2 }}{7}\).
C. \(\frac{{a\sqrt {14} }}{2}\).
D. \(\frac{{2a\sqrt {14} }}{7}\).

Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.

Advertisements (Quảng cáo)
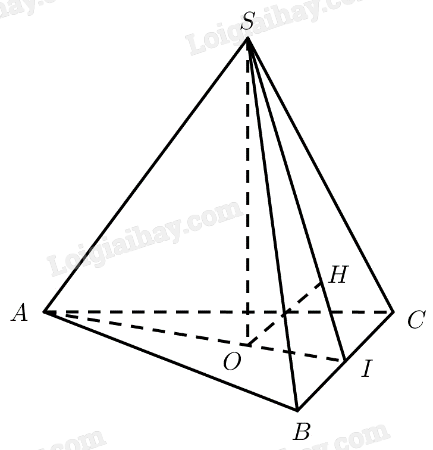
Gọi \(I\) là trung điểm của \(BC\), kẻ \(OH \bot SI\left( {H \in SI} \right)\).
\(ABC\) là tam giác đều \( \Rightarrow AI \bot BC\)
\(SO \bot \left( {ABC} \right) \Rightarrow SO \bot BC\)
\( \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot OH\)
Mà \(OH \bot SI\)
\( \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)
\(ABC\) là tam giác đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow OI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{3}\)
\(SO = a\sqrt 2 \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {14} }}{7}\)
Chọn A.
