
Tổng lượng mưa trong tháng 8 đo được tại một trạm quan trắc đặt tại Vũng Tàu từ năm 2002 đến năm 2020 được ghi lại như dưới đây (đơn vị: mm):
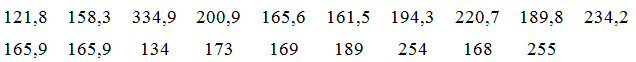
(Nguồn: Tổng cục Thống kê)
a) Xác định số trung bình, tứ phân vị và mốt của mẫu số liệu trên.
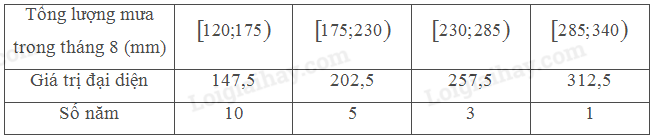
b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng số trung bình, tứ phân vị và mốt của mẫu số liệu ở bảng tần số ghép nhóm trên.

a) Sắp xếp dãy số liệu theo thứ tự không giảm và tìm tứ phân vị.
b) Đếm và lập bảng.
c) Sử dụng công thức tính số trung bình, tứ phân vị và mốt của mẫu số liệu ở bảng tần số ghép nhóm.

a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Số trung bình của số liệu là: \(\bar x \approx 192,41\)
Tứ phân vị thứ nhất là: \({x_5} = 165,6\)
Tứ phân vị thứ hai là: \({x_{10}} = 173\)
Tứ phân vị thứ ba là: \({x_{15}} = 220,7\)
Giá trị xuất hiện nhiều nhất là \({M_O} = 165,9\)
b)

c) Ta có:
Advertisements (Quảng cáo)
• Lượng mưa trung bình trong tháng 8 là:
\(\bar x = \frac{{10.147,5 + 5.202,5 + 3.257,5 + 1.312,5}}{{19}} \approx 188,03\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\).
Do đó: \({u_m} = 120;{n_{m - 1}} = 0;{n_m} = 10;{n_{m + 1}} = 5;{u_{m + 1}} - {u_m} = 175 - 120 = 55\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{120 - 0}}{{\left( {120 - 0} \right) + \left( {120 - 5} \right)}}.55 \approx 148,09\)
• Gọi \({x_1};{x_2};...;{x_{19}}\) là lượng mưa trong tháng 8 được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}}\end{array};{x_{11}},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {175;230} \right)}\end{array};{x_{16}},{x_{17}},{x_{18}} \in \begin{array}{*{20}{l}}{\left[ {230;285} \right)}\end{array};{x_{19}} \in \begin{array}{*{20}{l}}{\left[ {285;340} \right)}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{10}}\)
Ta có: \(n = 19;{n_m} = 10;C = 0;{u_m} = 120;{u_{m + 1}} = 175\)
Do \({x_{10}} \in \begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{\frac{{19}}{2} - 0}}{{10}}.\left( {175 - 120} \right) = 172,25\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_5}\).
Ta có: \(n = 19;{n_m} = 10;C = 0;{u_m} = 120;{u_{m + 1}} = 175\)
Do \({x_5} \in \begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{\frac{{19}}{4} - 0}}{{10}}.\left( {175 - 120} \right) = 146,125\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{16}}\).
Ta có: \(n = 19;{n_j} = 3;C = 10 + 5 = 15;{u_j} = 230;{u_{j + 1}} = 285\)
Do \({x_{16}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\left[ {230;285} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 230 + \frac{{\frac{{3.19}}{4} - 15}}{3}.\left( {285 - 230} \right) = 216,25\)
