
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?
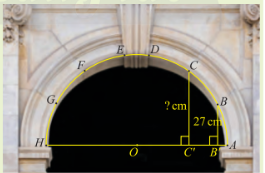

Dựa vào hình vẽ để giải quyết bài toán

Đặt chiều rộng cổng AH = d.
\( \Rightarrow OA = OB = \frac{1}{2}d\)
Advertisements (Quảng cáo)
Xét tam giác OBB’ có:
\(\sin \widehat {BOB’} = \frac{{BB’}}{{OB}} = \frac{{27}}{{\frac{d}{2}}} = \frac{{54}}{d}\)
Vì số đo cung AB = số đo cung BC nên số đo cung AC = 2.AB\( \Rightarrow \widehat {AOC} = 2\widehat {BOB’}\)
Xét tam giác OCC’ vuông tại C’ có:
\(\begin{array}{l}\sin \widehat {COC’} = \frac{{CC’}}{{OC}}\\ \Leftrightarrow CC’ = OC.\sin \widehat {COC’} = OC.\sin \left( {2\widehat {BOB’}} \right)\end{array}\)
Mà \(\sin \left( {2\widehat {BOB’}} \right) = 2.\sin \widehat {BOB’}.cos\widehat {BOB’}\)
Vậy để tính khoảng cách từ điểm C đến AH ta phải tìm được \(\sin \widehat {BOB’},cos\widehat {BOB’}\).
