Hoạt động 1
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) sau đây:
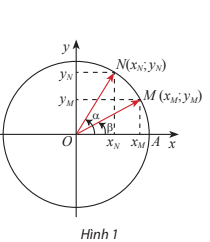
\(\overrightarrow {OM} .\overrightarrow {ON} = \left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {ON} } \right|.cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right)\)\( = cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right) = cos\left( {\alpha - \beta } \right)\)
\(\overrightarrow {OM} .\overrightarrow {ON} = {x_M}.{x_N} + {y_M}.{y_N}\)
Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.

Dựa vào hình vẽ và 2 công thức tính tích vô hướng để giải quyết

Ta có:
Advertisements (Quảng cáo)
\(cos\left( {\alpha - \beta } \right) = {x_M}.{x_N} + {y_M}.{y_N} = cos\alpha .cos\beta + \sin \alpha .\sin \beta \)
\(cos\left( {\alpha + \beta } \right) = cos\left( {\alpha - \left( { - \beta } \right)} \right) = cos\alpha .cos\left( { - \beta } \right) + \sin \alpha .\sin \left( { - \beta } \right) = cos\alpha .cos\beta - \sin \alpha .\sin \beta \)
Thực hành 1
Tính \(\sin \frac{\pi }{{12}}\) và \(\tan \frac{\pi }{{12}}\)

Sử dụng công thức \(\sin \left( {a - b} \right) = \sin a\cos b - \cos asinb\).
\(\tan \alpha = \frac{{\sin \alpha }}{{cos\alpha }}\)

Ta có:
\(\begin{array}{l}\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right) = \sin \frac{\pi }{3}cos\frac{\pi }{4} - cos\frac{\pi }{3}\sin \frac{\pi }{4}\\ = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} - \frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 6 - \sqrt 2 }}{4}\\{\rm{cos}}\frac{\pi }{{12}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\\\tan \frac{\pi }{{12}} = \frac{{\sin \frac{\pi }{{12}}}}{{{\rm{cos}}\frac{\pi }{{12}}}} = \frac{{\frac{{\sqrt 6 - \sqrt 2 }}{4}}}{{\frac{{\sqrt 6 + \sqrt 2 }}{4}}} = 2 - \sqrt 3 \end{array}\)
