Giải mục 1 trang 52, 53 Toán 11 tập 1 - Chân trời sáng tạo: Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều...

Hoạt động 1

Tìm điểm giống nhau của các dãy số sau:

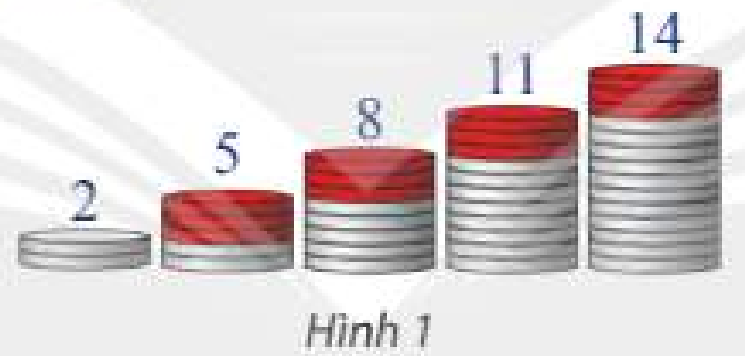
a) 2; 5; 8; 11; 14 (xem Hình 1).

b) 2; 4; 6; 8.

c) 5; 10; 15; 20; 25.

d) ‒5; ‒2; 1; 4; 7; 10.

Xem hai số hạng liên tiếp của dãy có liên hệ gì.

Ta thấy:

a) Số sau hơn số liền trước 3 đơn vị.

b) Số sau hơn số liền trước 2 đơn vị.

c) Số sau hơn số liền trước 5 đơn vị.

d) Số sau hơn số liền trước 3 đơn vị.

Điểm giống nhau của các dãy số này là hai số hạng liền nhau hơn kém nhau một số không đổi.

Thực hành 1

Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.

a) 3; 7; 11; 15; 19; 23.

b) Dãy số $\left( {{u_n}} \right)$ với ${u_n} = 9n - 9$.

c) Dãy số $\left( {{v_n}} \right)$ với ${v_n} = an + b$, trong đó $a$ và $b$ là các hằng số.

Biến đổi, đưa ${u_{n + 1}} = {u_n} + d$, khi đó dãy số là cấp số cộng có công sai $d$.

a) Dãy số: 3; 7; 11; 15; 19; 23 là cấp số cộng có công sai $d = 4$.

b) Ta có: ${u_{n + 1}} = 9\left( {n + 1} \right) - 9 = 9n + 9 - 9 = \left( {9n - 9} \right) + 9 = {u_n} + 9$.

Vậy dãy số $\left( {{u_n}} \right)$ là cấp số cộng có công sai ${\rm{d}} = 9$.

c) Ta có: ${v_{n + 1}} = a\left( {n + 1} \right) + b = an + a + b = \left( {an + b} \right) + a = {v_n} + a$.

Vậy dãy số $\left( {{v_n}} \right)$ là cấp số cộng có công sai ${\rm{d}} = a$.

Thực hành 2

Số đo ba góc của một tam giác vuông lập thành cấp số cộng. Tìm số đo ba góc đó.

Dựa vào tính chất:

‒ Tam giác vuông có một góc bằng ${90^ \circ }$.

‒ Tổng ba góc trong tam giác bằng ${180^ \circ }$.

Do tam giác đó là tam giác vuông nên có một góc bằng ${90^ \circ }$.

Giả sử hai góc còn lại của tam giác có số đo lần lượt là $a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)$.

Vì tổng ba góc trong tam giác bằng ${180^ \circ }$ nên ta có: $a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }$(1).

Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:

$b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }$ (2)

Từ (1) và (2) ta có hệ phương trình sau:

$\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.$

Vậy số đo ba góc của tam giác vuông đó lần lượt là: ${30^ \circ };{60^ \circ };{90^ \circ }$.

Vận dụng 1

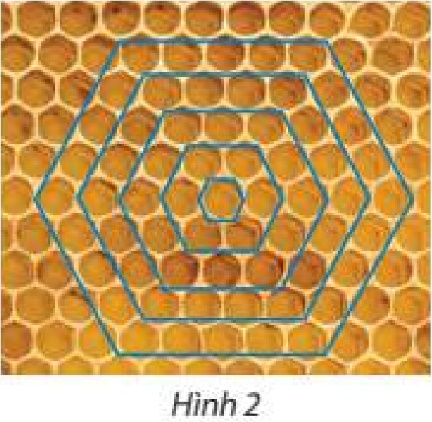
Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quanh vòng 2; cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.

Biến đổi, đưa ${u_{n + 1}} = {u_n} + d$, khi đó dãy số là cấp số cộng có công sai $d$.

Ta có: Dãy số chỉ số ô trên các vòng là: ${u_1} = 6;{u_2} = 12;{u_3} = 18;...$

Ta thấy: ${u_{n + 1}} = {u_n} + 6$

Vậy ô trên các vòng theo thứ tự tạo thành cấp số cộng có công sai ${\rm{d}} = 6$.