Hoạt động 1
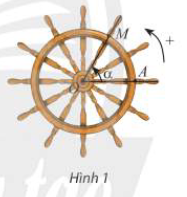
Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA.
a) Khi quay bánh lái ngược chiều kim đồng hồ ( Hình 1), cứ mỗi giây, bánh lái quay một góc \( {60^0}\). Bảng dưới đây cho ta góc quay \(\alpha \)của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hơp.

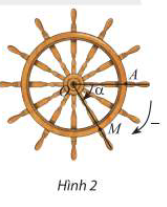
b) Nếu bánh lái được quay theo chiều ngược lại, nghĩa là quay cùng chiều kim đồng hồ ( Hình 2) với cùng tốc độ như trên, người ta ghi -\({60^ \circ }\)để chỉ góc mà thanh OM quay được sau mỗi giây. Bảng dưới đây cho ta góc quay \(\alpha \)của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.
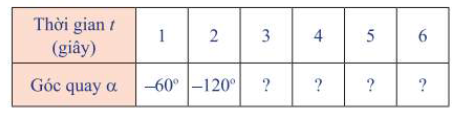

Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.

a)
|
Thời gian t (giây) |
1 |
2 |
3 |
4 |
5 |
6 |
|
Góc quay \(\alpha \) |
\({60^ \circ }\) |
\({120^ \circ }\) |
\({180^ \circ }\) |
\({240^ \circ }\) |
\({300^ \circ }\) |
\({360^ \circ }\) |
b)
|
Thời gian t (giây) |
1 |
2 |
3 |
4 |
5 |
6 |
|
Góc quay \(\alpha \) |
-\({60^ \circ }\) |
-\({120^ \circ }\) |
-\({180^ \circ }\) |
-\({240^ \circ }\) |
-\({300^ \circ }\) |
-\({360^ \circ }\) |
Thực hành 1
Advertisements (Quảng cáo)
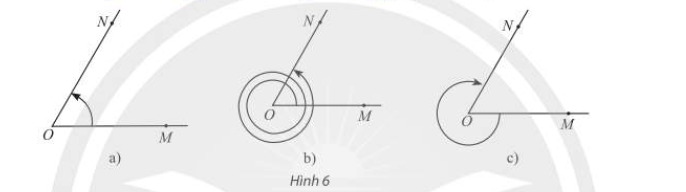
Cho \(\widehat {MON} = {60^ \circ }\). Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM,ON).

- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.
- Số đo của các góc lượng giác có cùng tia đầu Oa, và tia cuối Ob sai khác nhau một bội nguyên của \({360^ \circ }\)nên có công thức tổng quát là: \((Oa,Ob) = {\alpha ^ \circ } + k{360^ \circ }(k \in \mathbb{Z}),\)với \({\alpha ^ \circ }\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.

a) Số đo của góc lượng giác (OM,ON) trong Hình 6 là \({60^ \circ }\)
b) Số đo của góc lượng giác (OM,ON) trong Hình 6 là \({60^ \circ } + {2.360^ \circ } = {780^ \circ }\)
c) Số đo của góc lượng giác (OM,ON) trong Hình 6 là \(\frac{5}{6}.( - {360^ \circ }) = - {300^ \circ }\)
Công thức tổng quát của số đo góc lượng giác \((OM,ON) = {60^ \circ } + k{360^ \circ }(k \in \mathbb{Z})\)
Vận dụng 1
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là bao nhiêu độ?

- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.

Đổi 2 giờ 15 phút = \(\frac{9}{4}\)giờ.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là \(\frac{9}{4}.( - {360^ \circ }) = - {810^ \circ }\)
Hoạt động 2
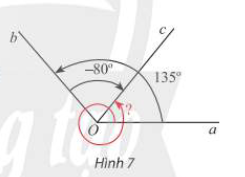
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.

- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.

a) Số đo của góc lượng giác (Oa,Ob) trong Hình 7 là \({135^ \circ } + n{.360^ \circ },(n \in \mathbb{Z})\)
Số đo của góc lượng giác (Ob,Oc) trong Hình 7 là \( - {80^ \circ } + m{.360^ \circ },(m \in \mathbb{Z})\)
Số đo của góc lượng giác (Oa,Oc) trong Hình 7 là \({415^ \circ } + k{.360^ \circ },(k \in \mathbb{Z})\)
b)
\(\begin{array}{l}(Oa,Ob) + (Ob,Oc) = {135^ \circ } + n{.360^ \circ } + ( - {80^ \circ }) + m{.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {55^ \circ } + (n + m){.360^ \circ } = {415^ \circ } + (n + m - 1){.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {415^ \circ } + k{.360^ \circ } = (Oa,Oc)\end{array}\)
với \(k = n + m - 1\,;n,m,k \in \mathbb{Z}\)
Vận dụng 2
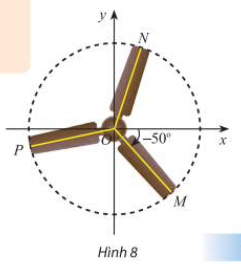
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox,ON) và (Ox,OP).

- Số đo của các góc lượng giác có cùng tia đầu Oa, và tia cuối Ob sai khác nhau một bội nguyên của \({360^ \circ }\)nên có công thức tổng quát là: \((Oa,Ob) = {\alpha ^ \circ } + k{360^ \circ }(k \in \mathbb{Z}),\)với \({\alpha ^ \circ }\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.

Công thức tổng quát số đo của góc lượng giác \((Ox,ON) = {70^ \circ } + k{360^ \circ }(k \in \mathbb{Z})\)
Công thức tổng quát số đo của góc lượng giác \((Ox,OP) = (Ox,OM) + (OM,OP) = - {50^ \circ } + ( - {120^ \circ }) + m{360^ \circ } = - {170^ \circ } + m{360^ \circ }\,\,\,\,,(m \in \mathbb{Z})\)
