Hoạt động 2
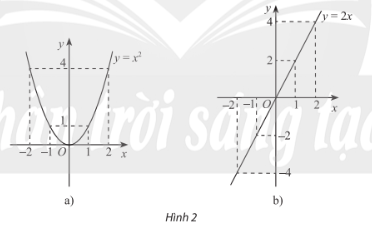
Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.

Quan sát đồ thị để trả lời.

* Hàm số \(y = {x^2}\)
Nhìn đồ thị ta thấy:
+ \(y(1) = y( - 1) = 1,y(2) = y( - 2) = 4\)
+ Đồ thị hàm số đối xứng qua trục Oy.
* Hàm số \(y = 2x\)
Nhìn đồ thị ta thấy:
+ \(y(1) = - y( - 1),y(2) = - y( - 2)\)
+ Đồ thị hàm số đối xứng qua điểm O.
Thực hành 1
Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ.

Cho hàm số y = f(x) có tập xác định là D. Hàm số f(x) được gọi là hàm số lẻ nếu \(\forall x \in D\)thì \( - x \in D\)và \(f( - x) = - f(x)\).

* Hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}}\)
Tập xác định \({\rm{D}} = \mathbb{R}\).
Với mọi \(x \in \mathbb{R}\)thì \( - x \in \mathbb{R}\) và \({\mathop{\rm s}\nolimits} {\rm{in}}\left( { - x} \right) = - {\mathop{\rm s}\nolimits} {\rm{in}}x\).
Vậy nên \(y = {\mathop{\rm s}\nolimits} {\rm{inx}}\) là hàm số lẻ.
* Hàm số \(y = \cot x\)
Tập xác định \({\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
Advertisements (Quảng cáo)
Với mọi \(x \in \mathbb{R}\)thì \( - x \in \mathbb{R}\) và \(\cot \left( { - x} \right) = - \cot x\).
Vậy nên \(y = \cot {\rm{x}}\) là hàm số lẻ.
Hoạt động 3
Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi \(x \in \mathbb{R}\).

Dựa vào tính chất
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha + k\pi } \right) = \cot \alpha \end{array}\)

Do \(\sin \left( {x + k2\pi } \right) = \sin x\),\(k \in \mathbb{Z}\).
\( \Rightarrow \sin \left( {x + 2\pi } \right) = \sin x\)
Nên \(T = 2\pi \).
Thực hành 2
Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T \( \ne \)0 sao cho với mọi \(x \in D\)ta có \(x \pm T \in D\) và\(f(x + T) = f(x)\)
Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Hàm số y = cosx
+ Tập xác định \({\rm{D}} = \mathbb{R}\).
+ Với mọi \(x \in \mathbb{R}\)ta có \(x \pm 2\pi \in D\) và\(\cos (x + 2\pi ) = \cos (x)\)
Vậy hàm số y = cosx là hàm tuần hoàn vỡi chu kì \(T = 2\pi \).
* Hàm số y = cotx
+ Tập xác định \({\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
+ Với mọi \(x \in \mathbb{R}\)ta có \(x \pm \pi \in D\) và\(\cot (x + \pi ) = \cot (x)\)
Vậy hàm số y = cosx là hàm tuần hoàn vỡi chu kì \(T = \pi \).
