Hoạt động 4
Cho một khối hộp chữ nhật với các kích thước là \(a,b,c\) đều là số nguyên dương. Về các mặt phẳng song song với các mặt của hình hộp và chia nó thành các khối lập phương có cạnh bằng 1 (Hình 11). Tìm số hình lập phương đơn vị có trong hình hộp.
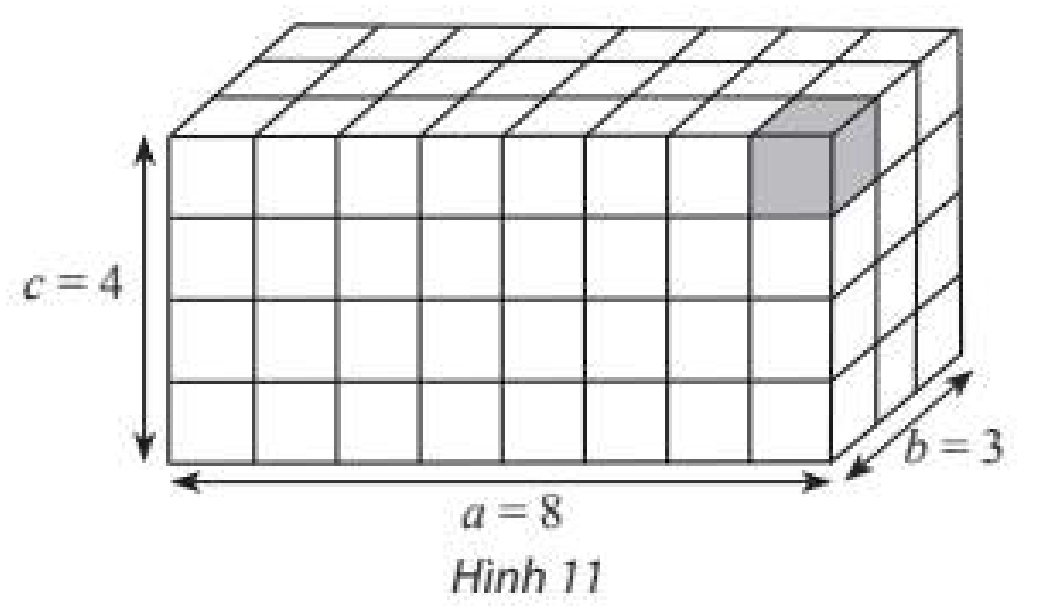

Quan sát hình ảnh và trả lời câu hỏi.

Số hình lập phương đơn vị có trong hình hộp là: \(abc\).
Hoạt động 5
Cho khối lăng trụ tam giác \(ABC.A’B’C’\) (Hình 14). Tìm cách chia khối lăng trụ thành ba khối chóp có cùng chiều cao và diện tích đáy.
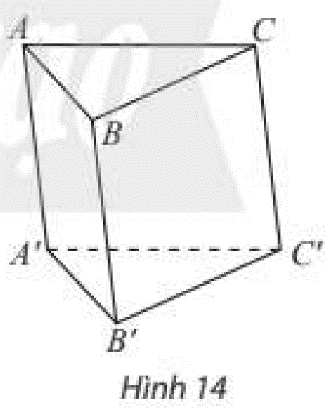

Chia khối lăng trụ thành ba khối chóp có đáy là một trong hai đáy của lăng trụ, đỉnh nằm trên đáy còn lại.

Chia khối lăng trụ tam giác \(ABC.A’B’C’\) thành ba khối chóp: \(A.A’B’C’,B’.ABC\) và \(C.A’B’C’\).
Thực hành 4
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.
Advertisements (Quảng cáo)
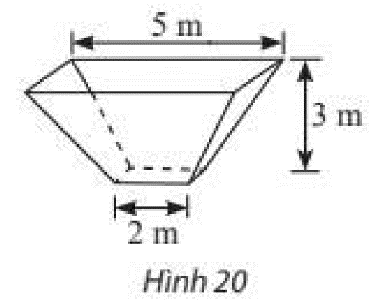

Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS’} + S’} \right)\).

Diện tích đáy lớn là: \(S = {5^2} = 25\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S’ = {2^2} = 4\left( {{m^2}} \right)\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.3\left( {25 + \sqrt {25.4} + 4} \right) = 39\left( {{m^3}} \right)\)
Vận dụng 3
Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.
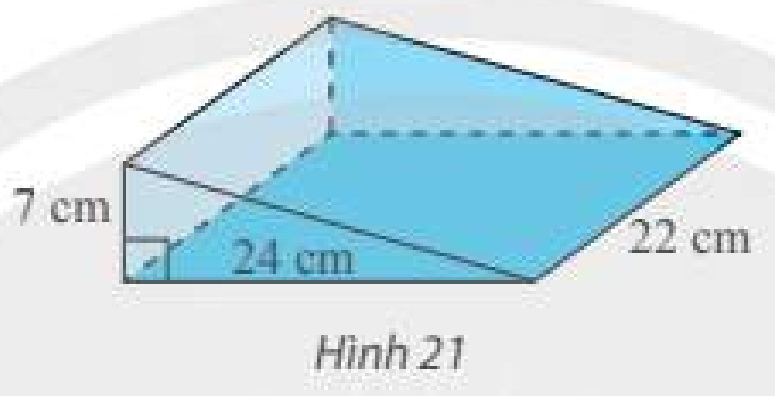

Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).

Diện tích đáy của lăng trụ là: \(\frac{1}{2}.7.24 = 84\left( {c{m^2}} \right)\)
Thể tích cái nêm hình lăng trụ đứng là: \(84.22 = 1848\left( {c{m^3}} \right)\)
