Cho hình lập phương \(ABCD.A’B’C’D’\) có \(AC’ = \sqrt 3 \). Khoảng cách giữa hai đường thẳng \(AB’\) và \(BC’\) bằng
A. \(\frac{1}{3}\).
B. \(\frac{{\sqrt 3 }}{3}\).
C. \(\frac{{\sqrt 3 }}{2}\).
D. \(\frac{1}{2}\)
Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này đến mặt phẳng song song chứa đường thẳng kia
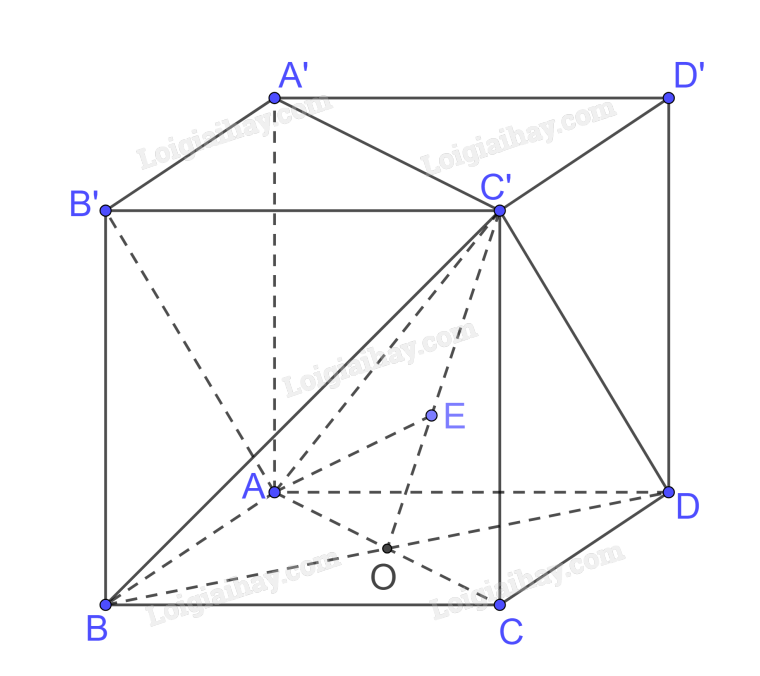
Gọi AC giao BD tại O
Ta có \(AC \bot BD,BD \bot AA’ \Rightarrow BD \bot \left( {ACC’A’} \right);BD \subset \left( {BDC’} \right) \Rightarrow \left( {ACC’A’} \right) \bot \left( {BDC’} \right)\)
Mà \(\left( {ACC’A’} \right) \cap \left( {BDC’} \right) = OC’\)
Trong (ACCA’) kẻ \(AE \bot OC’\)
Do đó \(AE \bot \left( {BDC’} \right)\)
Ta có AB’ // DC’ nên \(d\left( {AB’,BC’} \right) = d\left( {AB’,\left( {BDC’} \right)} \right) = d\left( {A,\left( {BDC’} \right)} \right) = AE\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {2A{B^2}} = AB\sqrt 2 \)
Xét tam giác ACC’ vuông tại C có
\(\begin{array}{l}A{C^2} + C{{C’}^2} = A{{C’}^2}\\ \Leftrightarrow {\left( {AB\sqrt 2 } \right)^2} + A{B^2} = 3\\ \Leftrightarrow 3A{B^2} = 3\\ \Leftrightarrow AB = 1\\ \Leftrightarrow AC = \sqrt 2 \end{array}\)
Xét tam giác OCC’ vuông tại C có \(C’O = \sqrt {C{{C’}^2} + O{C^2}} = \sqrt {{1^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = \frac{{\sqrt 6 }}{2}\)
Dễ dàng chứng minh
\( \Rightarrow \frac{{AE}}{{CC’}} = \frac{{AO}}{{C’O}} \Rightarrow AE = \frac{{AO.CC’}}{{C’O}} = \frac{{\frac{{\sqrt 2 }}{2}.1}}{{\frac{{\sqrt 6 }}{2}}} = \frac{{\sqrt 3 }}{3}\)
Đáp án B