
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số \(\frac{{SK}}{{SC}}\) bằng:
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{1}{4}\)
D. \(\frac{2}{3}\)

Áp dụng định lý Menelaus để tính tỉ số.

Advertisements (Quảng cáo)
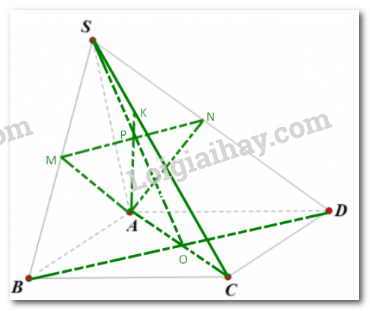
Gọi O là giao điểm AC và BD, gọi P là trung điểm MN
Ta có MN là đường trung bình tam giác SBD
Suy ra S, P, O thẳng hàng và P là trung điểm của SO
Do đó P thuộc SO hay P thuộc mp(SAC)
Trong mp(SAC), nối AP kéo dài cắt SC tại K
Suy ra K là giao điểm của SC và mp(AMN)
Áp dụng định lí Menelaus cho tam giác SOC:
\(\frac{{KS}}{{KC}} \times \frac{{CA}}{{AO}} \times \frac{{OP}}{{PS}} = 1\) suy ra \(\frac{{KS}}{{KC}} \times \frac{2}{1} \times 1 = 1\) suy ra \(\frac{{KS}}{{KC}} = \frac{1}{2}\)
Vậy \(\frac{{SK}}{{SC}} = \frac{1}{3}\)
Đáp án: B.
