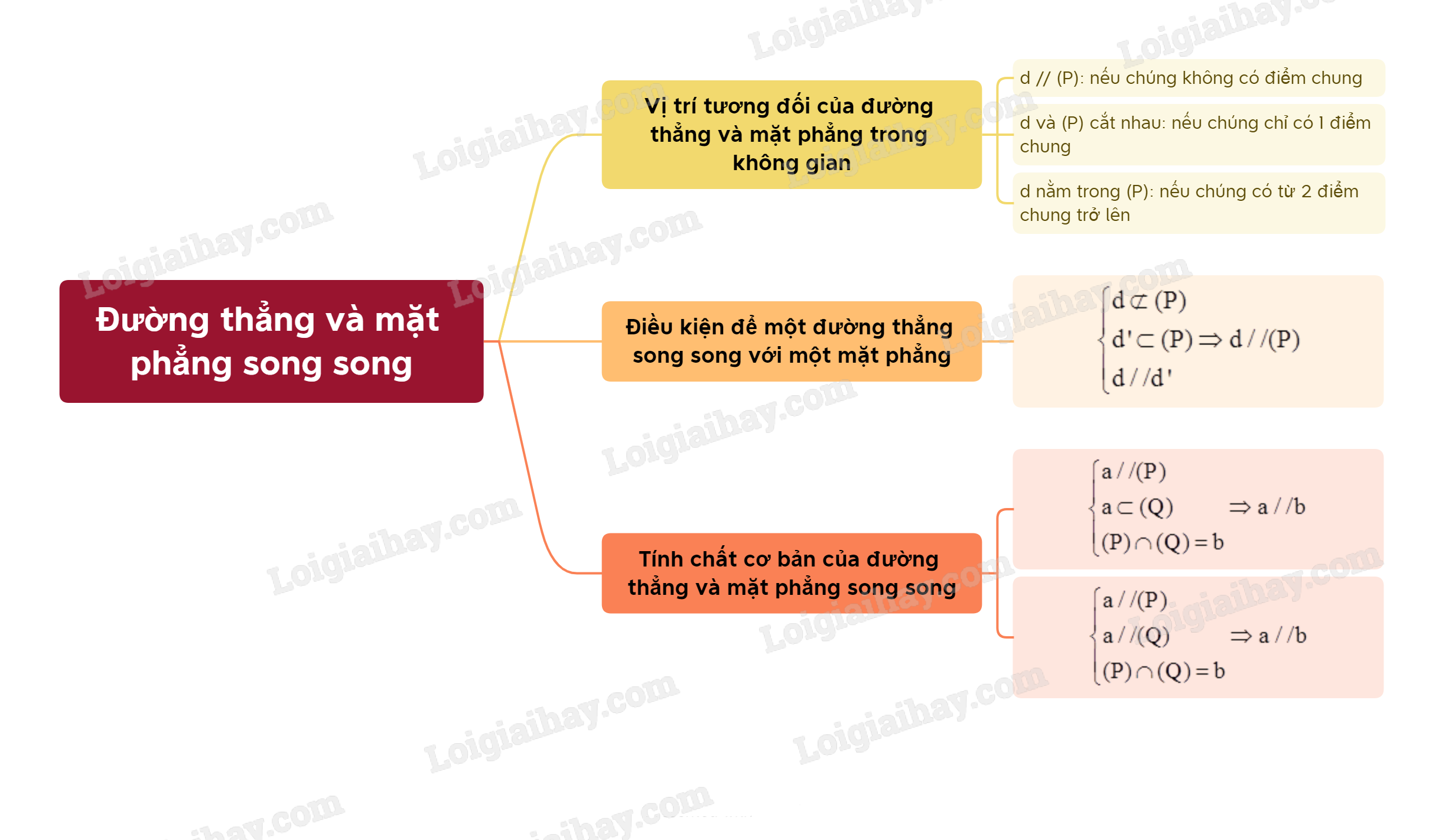
1. Đường thẳng song song với mặt phẳng
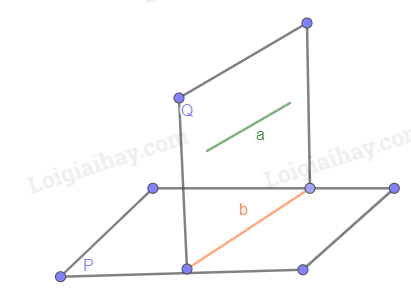
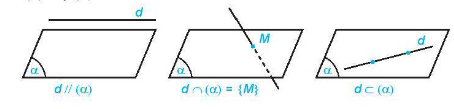
Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\). Nếu d và \(\left( \alpha \right)\) không có điểm chung thì ta nói d song song với \(\left( \alpha \right)\) hay \(\left( \alpha \right)\)song song với d. Kí hiệu là \(d//\left( \alpha \right)\)hay \(\left( \alpha \right)//d\).
*Nhận xét:
Nếu d và \(\left( \alpha \right)\) có một điểm chung duy nhất thì ta nói d và \(\left( \alpha \right)\) cắt nhau tại M. Kí hiệu \(d \cap \left( \alpha \right) = M\)hay \(d \cap \left( \alpha \right) = \left\{ M \right\}\).
Nếu d và \(\left( \alpha \right)\) có nhiều hơn 1 điểm chung thì ta nói d nằm trong \(\left( \alpha \right)\) hay \(\left( \alpha \right)\) chứa d. Kí hiệu \(d \subset \left( \alpha \right)\)hay \(\left( \alpha \right) \supset d\).
Advertisements (Quảng cáo)
2. Điều kiện và tính chất của đường thẳng song song với mặt phẳng
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì ta nói \(a//\left( P \right)\).
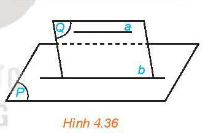
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b//a.