1. Hai mặt phẳng song song
Hai mặt \(\left( \alpha \right)\) và \(\left( \beta \right)\) được gọi là song song với nhau nếu chúng không có điểm chung. Kí hiệu \(\left( \alpha \right)\)// \(\left( \beta \right)\) hay \(\left( \beta \right)\)//\(\left( \alpha \right)\).
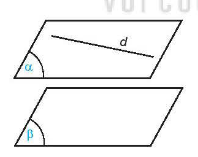
*Nhận xét: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( \beta \right)\\d \subset \left( \alpha \right)\end{array} \right. \Rightarrow d//\left( \beta \right)\).
2. Điều kiện và tính chất của hai mặt phẳng song song
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng \(\left( \beta \right)\)thì \(\left( \alpha \right)\)và \(\left( \beta \right)\)song song với nhau.
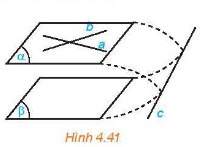
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
3. Định lí Thalès trong không gian
Advertisements (Quảng cáo)
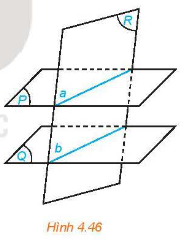
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
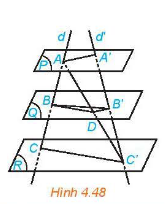
\(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{AC}}{{A’C’}}\)
4. Hình lăng trụ và hình hộp
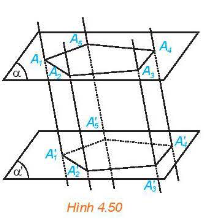
Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( {\alpha ‘} \right)\). Trên \(\left( \alpha \right)\) cho đa thức đa giác lồi \({A_1}{A_2}...{A_n}\). Qua các đỉnh\({A_1},{A_2},...,{A_n}\)vẽ các đường thẳng đôi một song song và cắt mặt phẳng \(\left( {\alpha ‘} \right)\)tại \({A_1}’,{A_2}’,...,{A_n}’\). Hình gồm hai đa giác\({A_1}{A_2}...{A_n}\), \({A_1}'{A_2}’...{A_n}’\) và các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\)được gọi là hình lăng trụ và kí hiệu là \({A_1}{A_2}...{A_n}.{A_1}'{A_2}’...{A_n}’\).
Các điểm \({A_1},{A_2},...,{A_n}\) và \({A_1}’,{A_2}’,...,{A_n}’\)được gọi là các đỉnh, các đoạn thẳng \({A_1}{A_1}’,{A_2}{A_2}’,...,{A_n}{A_n}’\)được gọi là các cạnh bên, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_1}\)và \({A_1}'{A_2}’,{A_2}'{A_3}’,...,{A_n}'{A_1}’\) gọi là cạnh đáy của hình trụ.
Hai đa giác \({A_1}{A_2}...{A_n}\)và \({A_1}'{A_2}’...{A_n}’\)được gọi là hai mặt đáy của hình lăng trụ.
Các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\) gọi là các mặt bên của hình trụ.
Hình lăng trụ tứ giác ABCD.A’B’C’D’ có hai đáy là hình bình hành được gọi là hình hộp.