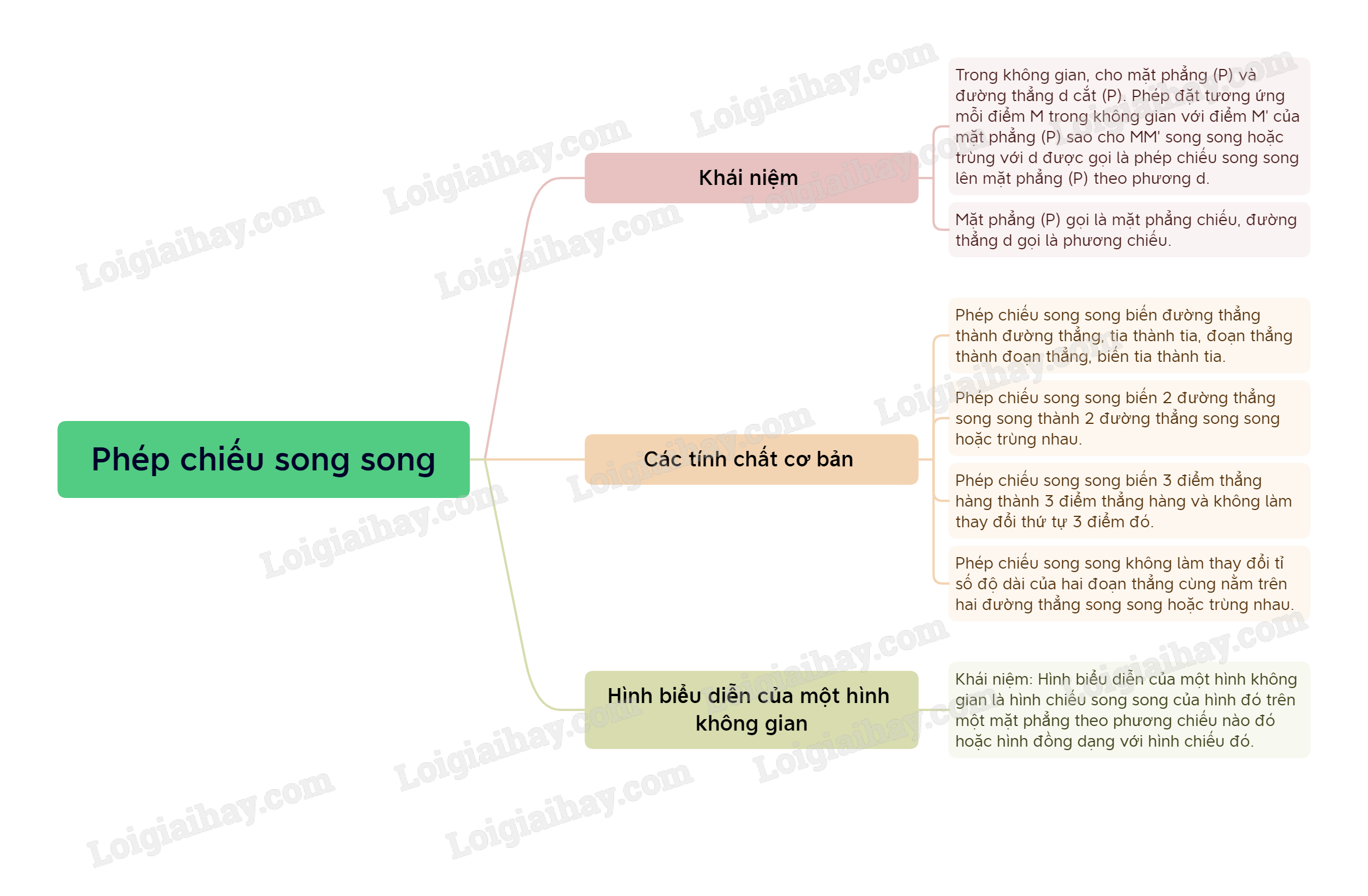
1. Phép chiếu song song
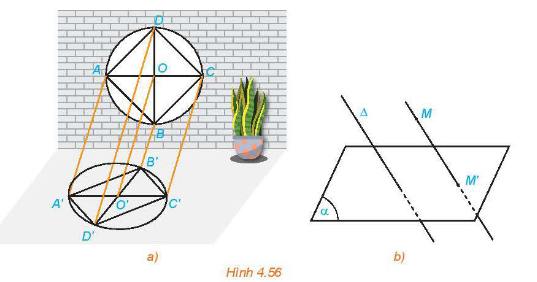
Cho mặt phẳng \(\left( \alpha \right)\)và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
- Nếu M thuộc\(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).
- Nếu M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).
- Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng \(\left( \alpha \right)\) theo phương \(\Delta \).
- Phép đặt tương ứng mỗi điểm M với hình chiếu M’ của nó được gọi là phép chiếu song song lên \(\left( \alpha \right)\)theo phương \(\Delta \).
- Mặt phẳng \(\left( \alpha \right)\) được gọi là mặt phẳng chiếu, phương \(\Delta \)gọi là phương chiếu.
- Cho hình \(\Re \), tập hợp các hình chiếu \(\Re ‘\)của các điểm M thuộc \(\Re \)qua phép chiếu song song được gọi là hình chiếu của \(\Re \) qua phép chiếu song song đó.
Advertisements (Quảng cáo)
2. Tính chất của phép chiếu song song
- Phép chiếu song song biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự 3 điểm đó.
- Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
- Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.
- Phép chiếu song song giữ nguyên tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.
3. Hình biểu diễn của một hình không gian
Hình biểu diễn của một hình không gian là hình chiếu song song của hình đó trên một mặt phẳng theo phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.