Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc và AB = a, BC = b, CD = c.. Câu 16 trang 103 SGK Hình học 11 Nâng cao - Bài 3: Đường thẳng vuông góc với mặt phẳng
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc và AB = a, BC = b, CD = c.
a. Tính độ dài AD.
b. Chỉ ra điểm cách đều A, B, C, D
c. Tính góc giữa đường thẳng AD và mặt phẳng (BCD), góc giữa đường thẳng AD và mặt phẳng (ABC).
Giải
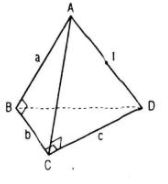
a. Ta có: CD ⊥ BC và CD ⊥ AB nên CD ⊥ (ABC)
mà AC ⊂ (ABC) do đó CD ⊥ AC.
Advertisements (Quảng cáo)
Trong tam giác vuông ABC ta có :
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)
Trong tam giác vuông ACD ta có :
\(A{D^2} = A{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\)
Suy ra : \(AD = \sqrt {{a^2} + {b^2} + {c^2}} \)
b. Ta có : \(AB \bot BC\,va\,AB \bot CD\) suy ra AB ⊥ (BCD) do đó AB ⊥ BD.
Gọi I là trung điểm AD ta có IC = IA = IB = ID.
Vậy I cách đều A, B, C, D