Bài 22. Tính các góc của tam giác \(ABC\), biết \(AB = \sqrt 2 cm\), \(AC =\sqrt 3 cm\) và đường cao \(AH = 1cm\). (Gợi ý : Xét trường hợp \(B, C\) nằm khác phía đối với \(H\) và trường hợp \(B, C\) nằm cùng phía đối với \(H\)).

Ta xét hai trường hợp :
a/ \(B\) và \(C\) nằm khác phía đối với \(H\)
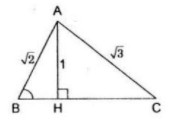
Trong tam giác vuông \(ABH\) ta có :
\(\sin B = {{AH} \over {AB}} = {1 \over {\sqrt 2 }}\)
Suy ra \(\widehat B = 45^\circ \) (chú ý rằng góc \(B\) nhọn)
Advertisements (Quảng cáo)
Trong tam giác \(ACH\) ta có :
\(\sin C = {{AH} \over {AC}} = {1 \over {\sqrt 3 }},\) suy ra \(\widehat C \approx 35^\circ 15’52\)
Từ đó \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 99^\circ 44’8\)
b/ \(B\) và \(C\) nằm cùng phía đối với \(H\)
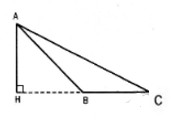
Tương tự như trên ta có :
\(\eqalign{
& \widehat {ABC} = 180^\circ - \widehat {ABH} = 180^\circ - 45^\circ = 135^\circ \cr
& \widehat C \approx 35^\circ 15’52 \cr} \)
Từ đó \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 9^\circ 44’8\)
