a. mp(BDA’) // mp(B’D’C)
b.Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C. Câu 37 trang 68 SGK Hình học 11 Nâng cao - Bài 4: Hai mặt phẳng song song
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng
a. mp(BDA’) // mp(B’D’C)
b.Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
c. G1 và G2 chia đoạn AC’ thành ba phần bằng nhau
d. Các trung điểm của sáu cạnh BC, CD, DD’, D’A’, A’B’,B’B cùng nằm trên một mặt phẳng

a) Chứng minh ( BDA’) // (B’D’C)
Ta có tứ giác BB’D’D và A’B’CD là các hình bình hành nên : BD // B’D’ và DA’ // B’C
⇒ hai mặt phẳng (BDA’) và (B’D’C) có các cặp đường thẳng cắt nhau và song song nhau từng đôi một nên chúng song song.
Vậy (BDA’) // (B’D’C).
b) Chứng minh G1 , G2 ∈ AC’
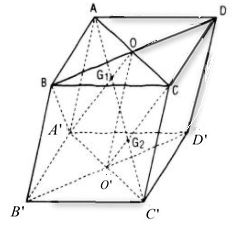
Gọi O, O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’.
Trong mặt phẳng (AA’C’C) gọi G1 , G2 lần lượt là giao điểm của AC’ với A’O và O’C. Ta chứng minh G1, G2 lần lượt là trong tâm của ∆A’BD và ∆CB’D’.
Thật vậy, ta có ∆G1OA đồng dạng ∆G1A’C’ ( vì AC // A’C’)
\( \Rightarrow {{{G_1}O} \over {{G_1}A’}} = {{OA} \over {A’C’}} = {1 \over 2} \Rightarrow {{A'{G_1}} \over {A’O}} = {2 \over 3}\)
⇒ G1 là trọng tâm ∆A’BD.
Advertisements (Quảng cáo)
Tương tự, G2 là trọng tâm ∆CB’D’. Vậy AC’ đi qua G1, G2 .
c) Chứng minh AG1 = G1G2 = G2C’
Theo câu trên , ta có:
\({{A{G_1}} \over {{G_1}C’}} = {{AO} \over {A’C’}} = {1 \over 2}\) ( vì ∆G1OA đồng dạng ∆G1A’C’) \( \Rightarrow A{G_1} = {1 \over 3}AC’\) (1)
Tương tự: \({{C'{G_2}} \over {{G_2}A}} = {{C’O’} \over {CA}} = {1 \over 2}\) ( vì ∆G2C’O’ đồng dạng ∆G2AC) \( \Rightarrow C'{G_2} = {1 \over 3}AC’\) (2)
Từ (1) và (2) suy ra: AG1 = G1G2 = G2C’.
d)
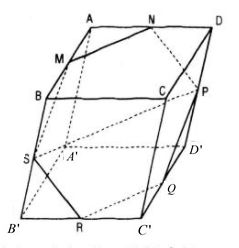
Gọi M, N, P, Q, S, R lần lượt là trung điểm của các cạnh AB, AD, DD’, C’D’, C’B’, B’B.
Ta có: \(\left\{ {\matrix{ {MN//BD} \cr {SP//BD} \cr } } \right. \Rightarrow MN//SP\)
Gọi (α) = (MN, SP)
Ta có : \(\left\{ {\matrix{ {PQ//DC’} \cr {MS//AB’} \cr } } \right. \Rightarrow PQ//MS\)
( vì DC’ // AB’)
⇒ PQ ⊂ (α) do đó Q ∈ (α).
Tương tự: QR // MN ⇒ QR ⊂ (α) do đó R ∈ (α).
Vậy M, N, P, Q, R, S ∈ (α).
Mặt khác vì \(\left\{ {\matrix{ {MS//AB’} \cr {NP//AD’} \cr } } \right.\) nên (MNPQRS) // (AB’D’).
