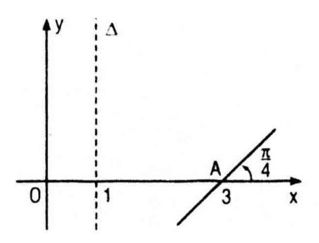
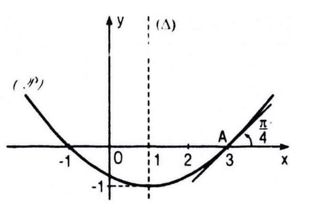
Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).

Đa thức phải tìm có dạng : \(P\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\)
Ta có: \(P’\left( x \right) = 2ax + b\)
Vì trục đối xứng (∆) có phương trình x = 1 nên : \( - {b \over {2a}} = 1\,\,\left( 1 \right)\)
Advertisements (Quảng cáo)
Vì đồ thị (P) đi qua điểm A(3 ; 0) nên ta có P(3) = 0, tức là:
\(9a + 3b + c = 0\,\,\left( 2 \right)\)
Vì hệ số góc của tiếp tuyến tại điểm A(3 ; 0) bằng \(\tan {\pi \over 4}\) nên ta có \(P’(3) = 1\), tức là :
\(6a + b = 1\,\left( 3 \right)\)
Giải hệ ba phương trình (1), (2) và (3) với ba ẩn số a, b và c, ta được :
\(\eqalign{ & a = {1 \over 4} \cr & b = - {1 \over 2} \cr & c = - {3 \over 4} \cr} \)
Vậy \(P\left( x \right) = {1 \over 4}{x^2} - {1 \over 2}x - {3 \over 4}\)
