Cho parabol (P) : \(y = {x^2}.\) Gọi M1 và M2 là hai điểm thuộc (P), lần lượt có hoành độ là x1 = -2 và x2 = 1.
Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình của tiếp tuyến đó.

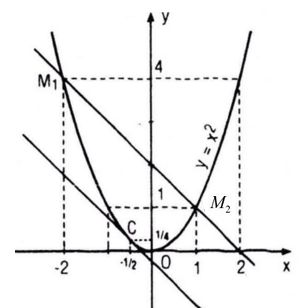
Các điểm M1 và M2 có tọa độ là M1(-2 ; 4); M2(1 ; 1)
Hệ số góc của cát tuyến M1M2 là \(\tan \varphi = {{\Delta y} \over {\Delta x}} = {{4 - 1} \over { - 2 - 1}} = - 1\)
Advertisements (Quảng cáo)
Vì tiếp tuyến tại điểm \(C\left( {{x_0};x_0^2} \right)\) song song với cát tuyến M1M2 nên ta có :
\(y’\left( {{x_0}} \right) = - 1 \Leftrightarrow 2{x_0} = - 1 \Leftrightarrow {x_0} = {{ - 1} \over 2},\)
Suy ra tọa độ của điểm C là \(\left( { - {1 \over 2};{1 \over 4}} \right)\)
Vậy phương trình tiếp tuyến phải tìm là :
\(y = \left( { - 1} \right)\left( {x + {1 \over 2}} \right) + {1 \over 4} \Leftrightarrow y = - x - {1 \over 4}\)
