Bài 2. Cho tứ diện \(ABCD\) có hai mặt \(ABC\) và \(BCD\) là hai tam giác cân có chung cạnh đáy \(BC\).Gọi \(I\) là trung điểm của cạnh \(BC\).
a) Chứng minh rằng \(BC\) vuông góc với mặt phẳng \(ADI\).
b) Gọi \(AH\) là đường cao của tam giác \(ADI\), chứng minh rằng \(AH\) vuông góc với mặt phẳng \(BCD\).

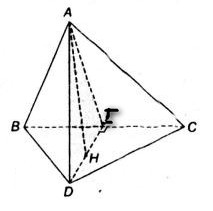
a) Tam giác \(ABC\) cân tại \(A\) nên ta có đường trung tuyến ứng với cạnh đáy đồng thời là đường cao do đó: \(AI\bot BC\)
Tương tự ta có: \(DI\bot BC\)
Advertisements (Quảng cáo)
Ta có:
$$\left. \matrix{
AI \bot BC \hfill \cr
DI \bot BC \hfill \cr
AI \cap DI = {\rm{\{ }}I{\rm{\} }} \hfill \cr} \right\} \Rightarrow BC \bot (ADI)$$
b) Ta có \(AH\) là đường cao của tam giác \(ADI\) nên \(AH\bot DI\)
Mặt khác: \(BC\bot (ADI)\) mà \(AH\subset (ADI)\) nên \(AH\bot BC\)
Ta có
$$\left. \matrix{
AH \bot BC \hfill \cr
AH \bot DI \hfill \cr
BC \cap DI = {\rm{\{ }}I{\rm{\} }} \hfill \cr} \right\} \Rightarrow AH \bot (BCD)$$
