Bài 4. Cho tứ diện \(OABC\) có ba cạnh \(OA, OB, OC\) đôi một vuông góc. Gọi \(H\) là chân đường vuông góc hạ từ \(O\) tới mặt phẳng \((ABC)\). Chứng minh rằng:
a) H là trực tâm của tam giác \(ABC\);
b) \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\)
Hướng dẫn.
(h.3.32)
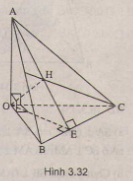
a) \(H\) là hình chiếu của \(O\) trên mp \((ABC)\) nên \(OH ⊥ (ABC) \Rightarrow OH ⊥ BC\). (1)
Mặt khác: \(OA ⊥ OB\), \(OA ⊥ OC\)
Advertisements (Quảng cáo)
\(\Rightarrow OA ⊥ (OBC) \Rightarrow OA ⊥ BC\) (2)
Từ (1) và (2) suy ra \(BC ⊥ (AOH) \Rightarrow BC ⊥ AH\). Chứng minh tương tự ta được \(AB ⊥ CH \)
\(\Rightarrow H\) là trực tâm của tam giác \(ABC\).
b) Trong mặt phẳng \((ABC)\) gọi \(E = AH ∩ BC\), \(OH ⊥ (ABC)\), \(AE ⊂ (ABC) \Rightarrow OH ⊥ AE\) tại \(H\);
\(OA ⊥ (ABC), OE ⊂ (ABC) \Rightarrow OA ⊥ OE\) tức là \(OH\) là đường cao của tam giác vuông \(OAE\).
Mặt khác \(OE\) là đường cao của tam giác vuông \(OBC\)
Do đó: \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OE^{2}} =\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\)
Nhận xét: Biểu thức này là mở rộng của công thức tính đường cao thuộc cạnh huyền của tam giác vuông: \(\frac{1}{h^{2}}=\frac{1}{b^{2}}+\frac{1}{c^{2}} .\)
