Bài 5. Trên mặt phẳng \((α)\) cho hình bình hành \(ABCD\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\). \(S\) là một điểm nằm ngoài mặt phẳng \((α)\) sao cho \(SA = SC, SB = SD\). Chứng minh rằng:
a) \(SO ⊥ (α)\);
b) Nếu trong mặt phẳng \((SAB)\) kẻ \(SH\) vuông góc với \(AB\) tại \(H\) thì \(AB\) vuông góc mặt phẳng \((SOH)\).

(H.3.33)
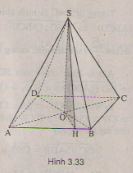
a) \(SA = SC\) nên tam giác \(SAC\) cân tại \(S\).
\(O\) là trung điểm của \(AC\) nên \(SO\) là đường trung tuyến đồng thời là đường cao của tam giác cân nên \(SO\bot AC\)
Advertisements (Quảng cáo)
Chứng minh tương tự ta có: \(SO\bot BD\)
Ta có:
$$\left. \matrix{
SO \bot BD \hfill \cr
SO \bot AC \hfill \cr
BD \cap AC = {\rm{\{ O\} }} \hfill \cr} \right\} \Rightarrow SO \bot (ABCD)$$
Hay \(SO ⊥ mp(α)\).
b) \(SO ⊥ (ABCD) \Rightarrow SO ⊥ AB\) (1)
Mà \(SH ⊥ AB\) (2)
Từ (1) và (2) suy ra \( AB ⊥ (SOH)\).
