Bài 5. Cho hàm số \(f(x) = \frac{x+2}{x^{2}-9}\) có đồ thị như trên hình 53.
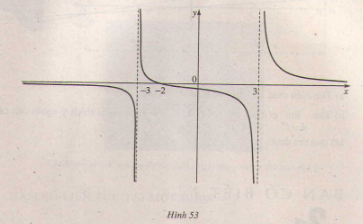
a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi \(x → -∞\), \(x → 3^-\) và \(x → -3^+\)
b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
\(\underset{x\rightarrow -\infty }{\lim} f(x)\) với \(f(x)\) được xét trên khoảng \((-\infty; -3)\),
\(\underset{x\rightarrow 3^{-}}{\lim} f(x)\) với \(f(x)\) được xét trên khoảng \((-3,3)\),
\(\underset{x\rightarrow -3^{+}}{lim} f(x)\) với \(f(x)\) được xét trên khoảng \((-3; 3)\).
Advertisements (Quảng cáo)
Hướng dẫn giải
a) Quan sát đồ thị ta thấy \(x → -∞\) thì \(f(x) → 0\); khi \(x → 3^-\) thì \(f(x) → -∞\);
khi \(x → -3^+\) thì \(f(x) → +∞\).
b) \(\underset{x\rightarrow -\infty }{lim} f(x) = \underset{x\rightarrow -\infty }{lim}\) \(\frac{x+2}{x^{2}-9}\) = \(\underset{x\rightarrow -\infty }{lim}\) \(\frac{\frac{1}{x}+\frac{2}{x^{2}}}{1-\frac{9}{x^{2}}} = 0\).
\(\underset{x\rightarrow 3^{-}}{lim} f(x) = \underset{x\rightarrow 3^{-}}{lim}\)\(\frac{x+2}{x^{2}-9}\) = \(\underset{x\rightarrow 3^{-}}{lim}\)\(\frac{x+2}{x+3}.\frac{1}{x-3} = -∞ \) vì \(\underset{x\rightarrow 3^{-}}{lim}\)\(\frac{x+2}{x+3}\) = \(\frac{5}{6} > 0\) và \(\underset{x\rightarrow 3^{-}}{\lim} \frac{1}{x-3} = -∞\).
\(\underset{x\rightarrow -3^{+}}{lim} f(x) =\) \(\underset{x\rightarrow -3^{+}}{lim}\) \(\frac{x+2}{x^{2}-9}\) = \(\underset{x\rightarrow -3^{+}}{lim}\) \(\frac{x+2}{x-3}\) . \(\frac{1}{x+3} = +∞\)
vì \(\underset{x\rightarrow -3^{+}}{lim}\) \(\frac{x+2}{x-3}\) = \(\frac{-1}{-6}\) = \(\frac{1}{6} > 0\) và \(\underset{x\rightarrow -3^{+}}{lim}\) \(\frac{1}{x+3} = +∞\).
