Bài 6 trang 105 sgk hình học 11: Bài 3. Đường thẳng vuông góc với mặt phẳng.. Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phẳng (ABCD)...
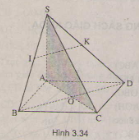
Bài 6. Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) và có cạnh \(SA\) vuông góc với mặt phẳng \((ABCD)\). Gọi \(I\) và \(K\) là hai điểm lần lượt lấy trên hai cạnh \(SB\) và \(SD\) sao cho \(\frac{SI}{SB}=\frac{SK}{SD}.\) Chứng minh:
a) \(BD\) vuông góc với \(SC\);
b) \(IK\) vuông góc với mặt phẳng \((SAC)\).
(H.3.34)
Advertisements (Quảng cáo)
a) \(ABCD\) là hình thoi nên \(AC\bot BD\) (1)
Theo giả thiết: \(SA\bot (ABCD)\Rightarrow SA\bot BD\) (2)
Từ (1) và (2) suy ra \(BD ⊥ (SAC)\) \(\Rightarrow BD ⊥ SC\).
b) Theo giả thiết \(\frac{SI}{SB}=\frac{SK}{SD}\) theo định lí ta lét ta có \(IK//BD\)
Theo a) ta có: \(BD ⊥ (SAC)\) do đó \( IK ⊥ (SAC)\).