Bài 9 trang 80 sách giáo khoa hình học 11: Ôn tập Chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song. Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các nửa đường thẳng song song với nhau lần lượt đi qua B, C, D và nằm về một phía của mặt phẳng (ABCD) đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A và cắt Bx, Cy, Dz lần lượt tại B', C', D' với BB'=2, DD'=4. Khi đó CC' bằng:
Bài 9. Cho hình bình hành \(ABCD\). Gọi \(Bx, Cy, Dz\) là các nửa đường thẳng song song với nhau lần lượt đi qua \(B, C, D\) và nằm về một phía của mặt phẳng \((ABCD)\) đồng thời không nằm trong mặt phẳng \((ABCD)\). Một mặt phẳng đi qua \(A\) và cắt \(Bx, Cy, Dz\) lần lượt tại \(B’, C’, D’\) với \(BB’=2, DD’=4\). Khi đó \(CC’\) bằng:
(A) 3
(B) 4
(C) 5
(D) 6
Giải
Advertisements (Quảng cáo)
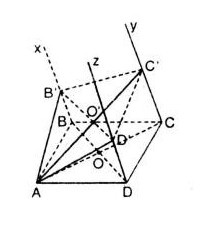
Gọi \(O,O’\) lần lượt là tâm của hình bình hành \(ABCD ,AB’C’D’\).
Ta có: \(BB’+DD’=2OO’=CC’\)
\(\Rightarrow CC’=6\)
Đáp án là D
baitapsgk.com
