Câu hỏi/bài tập:

Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 4} \) bằng:
A. 2.
B. 4.
C. 0.
D. 1.

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
Advertisements (Quảng cáo)
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.

Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = \frac{{{{\left( {{x^2} + 4} \right)}^\prime }}}{{2\sqrt {{x^2} + 4} }} = \frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + 4} }} = \frac{{\rm{x}}}{{\sqrt {{x^2} + 4} }}\)
\(y’ = 0\) khi \(x = 0\).
Bảng biến thiên của hàm số:
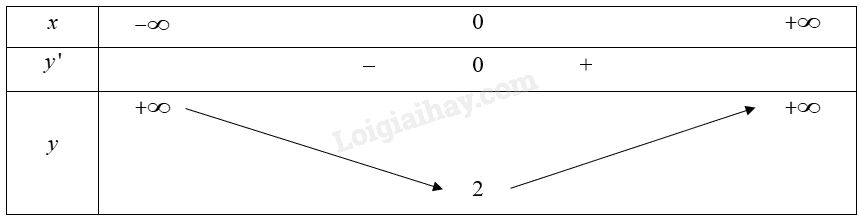
Căn cứ vào bảng biến thiên, ta có: \(\min f\left( x \right) = 2\) tại \({\rm{x}} = 0\).
Chọn A.
