Câu hỏi/bài tập:

Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình
\(s\left( t \right) = {t^3} - 6{t^2} + 14t + 1\)
trong đó \(t\) tính bằng giây và \(s\) tính bằng mét. Trong khoảng thời gian nào của 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên?

Xét hàm số \(v\left( t \right) = s’\left( t \right)\) trên đoạn \(\left[ {0;5} \right]\), lập bảng biến thiên và tìm khoảng đồng biến của hàm số.

Advertisements (Quảng cáo)
Vận tốc tức thời của chất điểm tại thời điểm \(t\) là: \(v\left( t \right) = s’\left( t \right) = 3{t^2} - 12t + 14\).
Xét hàm số \(v\left( t \right) = 3{t^2} - 12t + 14\) trên đoạn \(\left[ {0;5} \right]\).
Ta có: \(v’\left( t \right) = 6t - 12\).
\(v’\left( t \right) = 0\) khi \(t = 2\).
Bảng biến thiên của hàm số:
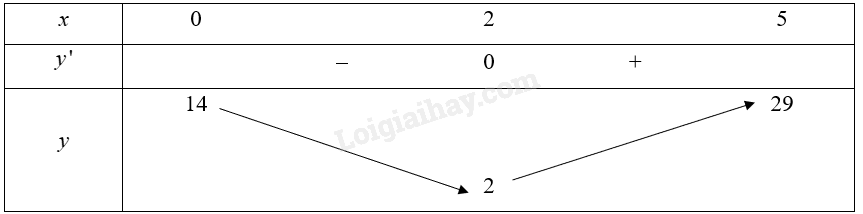
Vậy hàm số đồng biến trên khoảng \(\left( {2;5} \right)\).
Vậy trong khoảng thời gian từ 2 giây đến 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên.
