Câu hỏi/bài tập:

Khối lượng riêng \(S\left( {kg/d{m^3}} \right)\) của nước phụ thuộc vào nhiệt độ \(T\left( {^ \circ C} \right)\) được cho bởi công thức:
\(S = \frac{{5,755}}{{{{10}^8}}}{T^3} - \frac{{8,521}}{{{{10}^6}}}{T^2} + \frac{{6,540}}{{{{10}^5}}}T + 0,99987\) với \(0 < T \le 25\)
(Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
a) Tính khối lượng riêng của nước ở nhiệt độ \({25^ \circ }C\).
b) Ở nhiệt độ nào thì khối lượng riêng của nước là lớn nhất?

Xét hàm số \(S\) trên nửa khoảng \(\left( {0;25} \right]\), lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.

Advertisements (Quảng cáo)
a) Với \(T = 25\), ta có:
\(S\left( {25} \right) = \frac{{5,755}}{{{{10}^8}}}{.25^3} - \frac{{8,521}}{{{{10}^6}}}{.25^2} + \frac{{6,540}}{{{{10}^5}}}.25 + 0,99987 \approx 0,99708\left( {kg/d{m^3}} \right)\)
b) Xét hàm số \(S = \frac{{5,755}}{{{{10}^8}}}{T^3} - \frac{{8,521}}{{{{10}^6}}}{T^2} + \frac{{6,540}}{{{{10}^5}}}T + 0,99987\) trên nửa khoảng \(\left( {0;25} \right]\).
Ta có:
\(S’ = \frac{{5,755}}{{{{10}^8}}}.3{T^2} - \frac{{8,521}}{{{{10}^6}}}.2T + \frac{{6,540}}{{{{10}^5}}} = \frac{{17,265}}{{{{10}^8}}}.{T^2} - \frac{{17,042}}{{{{10}^6}}}.T + \frac{{6,540}}{{{{10}^5}}}\)
\(S’ = 0\) khi \(t \approx 4\).
Bảng biến thiên của hàm số:
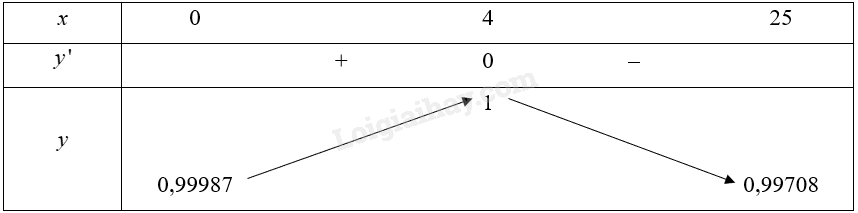
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\max }\limits_{\left( {0;25} \right]} S = 1\) tại \(t = 4\).
Vậy ở nhiệt độ \({4^ \circ }C\) thì khối lượng riêng của nước là lớn nhất.
