
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f’\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f’\left( x \right)\), hãy cho biết:
a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\);
b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
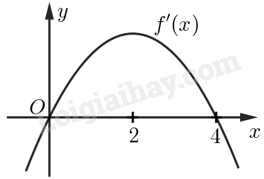

Ý a: Quan sát đồ thị để xác định dấu của đạo hàm, từ đó biết được các khoảng đồng biến, nghịch biến của hàm số.
Advertisements (Quảng cáo)
Ý b: Xác định các điểm trên đồ thị mà tại đó đạo hàm đổi dấu, đó chính là các điểm cực trị của hàm số.

a) Từ đồ thị ta có:
\(f’\left( x \right) > 0{\rm{ }}\forall {\rm{x}} \in \left( {0;4} \right)\) nên hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0;4} \right)\).
\(f’\left( x \right)
b) Ta có hàm số \(f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Vì \(f’\left( x \right)\) đổi dấu từ âm sang dương khi \(x\) đi qua \(0\) nên hàm số \(f\left( x \right)\) đạt cực tiểu tại \(x = 0\); \(f’\left( x \right)\) đổi dấu từ dương sang âm khi \(x\) đi qua \(4\) nên hàm số \(f\left( x \right)\) đạt cực đại tại \(x = 4\)
