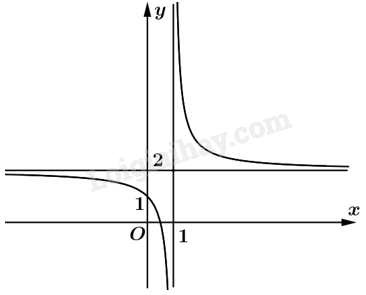
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{3x + 5}}{{x + 2}}\);
b) \(y = \frac{{2x - 1}}{{x - 1}}\).

+ Tìm tập xác định của hàm số.
+ Khảo sát sự biến thiên của hàm số: Tính đạo hàm, tìm các khoảng đồng biến, nghịch biến của đồ thị, tìm các điểm cực trị, cực trị, tiệm cận, ghi kết quả tìm được vào bảng biến thiên.
+ Vẽ đồ thị dựa vào bảng biến thiên, khi vẽ lưu ý đến tính đối xứng, tọa độ giao điểm với các trục.

a) Tập xác định: \(\mathbb{R}\backslash \left\{ { - 2} \right\}\)
Sự biến thiên:
+ Ta có \(y’ = \frac{1}{{{{\left( {x + 2} \right)}^2}}} > 0\) với mọi \(x \ne - 2\).
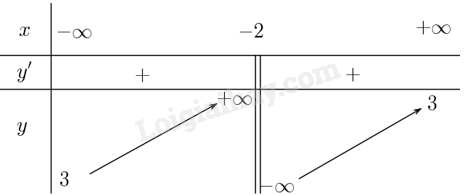
+ Hàm số đồng biến trên từng khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
+ Hàm số không có cực trị.
+ Tiệm cận: \(\mathop {\lim }\limits_{x \to + \infty } = 3\) suy ra tiệm cận ngang là đường thẳng \(y = 3\); \(\mathop {\lim }\limits_{x \to - {2^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to - {2^ - }} y = - \infty \) suy ra tiệm cận đứng là đường thẳng \(x = - 2\).
Advertisements (Quảng cáo)
+ Bảng biến thiên:
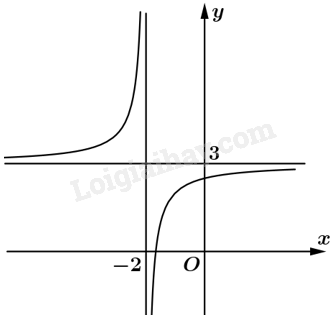
Đồ thị: Đồ thị của hàm số cắt trục tung tại điểm \(\left( {0;\frac{5}{2}} \right)\), cắt trục hoành tại hai điểm \(\left( {\frac{{ - 5}}{3};0} \right)\) và \(\left( {3;0} \right)\). Đồ thị nhận \(\left( { - 2;3} \right)\) làm tâm đối xứng. Hai trục đối xứng của hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận.
b) Tập xác định: \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Sự biến thiên:
+ Ta có \(y’ = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}}
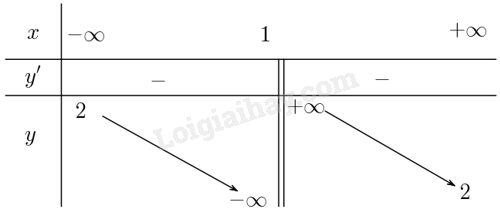
+ Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
+ Hàm số không có cực trị.
+ Tiệm cận: \(\mathop {\lim }\limits_{x \to + \infty } y = 2\) suy ra tiệm cận ngang là đường thẳng \(y = 2\); \(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \) suy ra tiệm cận đứng là đường thẳng \(x = 1\).
+ Bảng biến thiên:
Đồ thị: Đồ thị của hàm số cắt trục tung tại điểm \(\left( {0;1} \right)\), cắt trục hoành tại điểm \(\left( {\frac{1}{2};0} \right)\), đồ thị có tâm đối xứng là điểm \(\left( {1;2} \right)\). Hai trục đối xứng của hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận.