
Cho hình lập phương \(ABCD.A’B’C’D’\) có độ dài mỗi cạnh bằng 1. Xét hệ tọa độ \(Oxyz\) gắn với hình lập phương như hình vẽ bên.
a) Tìm tọa độ các đỉnh của hình lập phương.
b) Tìm tọa độ trọng tâm \(G\) của tam giác \(B’CD’\).
c) Chứng minh rằng ba điểm \(O,G,A\) thẳng hàng.
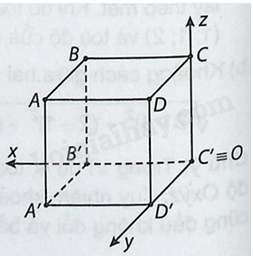

Ý a: Tìm tọa độ các đỉnh thuộc tia \(Ox,Oy,Oz\) trước, sau đó sử dụng các đẳng thức vectơ bằng nhau để tìm các điểm còn lại. Chú ý sử dụng giả thiết cạnh hình lập phương bằng 1.
Ý b: Dùng công thức tìm tọa độ trọng tâm.
Advertisements (Quảng cáo)
Ý c: Chứng minh \(\overrightarrow {OA} \) và \(\overrightarrow {OG} \) cùng phương bằng đẳng thức \(\overrightarrow {OA} = k\overrightarrow {OG} \).

a) Ta có gốc tọa độ là \(C’\) nên \(C’\left( {0;0;0} \right)\); \(B’\) thuộc tia \(Ox\) và \(OB’ = 1\) nên \(B’\left( {1;0;0} \right)\); \(D’\) thuộc tia \(Oy\) và \(OD’ = 1\) nên \(D’\left( {0;1;0} \right)\); \(C\) thuộc tia \(Oz\) và \(OC = 1\) nên \(C\left( {0;0;1} \right)\).
Ta có \(\overrightarrow {C’C} = \overrightarrow {D’D} \Leftrightarrow \left\{ \begin{array}{l}0 = {x_D}\\0 = {y_D} - 1\\1 = {z_D}\end{array} \right. \Leftrightarrow D\left( {0;1;1} \right)\); \(\overrightarrow {B’B} = \overrightarrow {C’C} \Leftrightarrow \left\{ \begin{array}{l}{x_B} - 1 = 0\\{y_B} = 0\\{z_B} = 1\end{array} \right. \Leftrightarrow B\left( {1;0;1} \right)\);
\(\overrightarrow {B’A’} = \overrightarrow {C’D’} \Leftrightarrow \left\{ \begin{array}{l}{x_{A’}} - 1 = 0\\{y_{A’}} = 1\\{z_{A’}} = 0\end{array} \right. \Leftrightarrow A’\left( {1;1;0} \right)\); \(\overrightarrow {A’A} = \overrightarrow {C’C} \Leftrightarrow \left\{ \begin{array}{l}{x_A} - 1 = 0\\{y_A} - 1 = 0\\{z_A} = 1\end{array} \right. \Leftrightarrow A\left( {1;1;1} \right)\).
Vậy \(A\left( {1;1;1} \right)\), \(B\left( {1;0;1} \right)\), \(C\left( {0;0;1} \right)\), \(D\left( {0;1;1} \right)\), \(A’\left( {1;1;0} \right)\), \(B’\left( {1;0;0} \right)\), \(C’\left( {0;0;0} \right)\)
và \(D’\left( {0;1;0} \right)\).
b) Ta có \(B’\left( {1;0;0} \right)\), \(C\left( {0;0;1} \right)\) và \(D’\left( {0;1;0} \right)\) suy ra \(G\left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\).
c) Ta có \(\overrightarrow {OG} = \left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\); \(\overrightarrow {OA} = \left( {1;1;1} \right)\). Suy ra \(\overrightarrow {OA} = 3\overrightarrow {OG} \). Vậy ba điểm \(O,G,A\) thẳng hàng.
