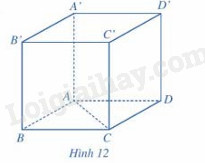
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính
a.\(\overrightarrow {A’B} .\overrightarrow {D’C} ;\overrightarrow {D’A} .\overrightarrow {BC} \)
b,Các góc \(\left( {\overrightarrow {A’D} ,\overrightarrow {B’C’} } \right);\left( {\overrightarrow {AD’,} \overrightarrow {BD} } \right)\)
Vẽ hình
Áp dụng phương pháp tích vô hướng của hai vecto trong không gian
a, .\(\overrightarrow {A’B} .\overrightarrow {D’C} = \left( {\overrightarrow {A’B’} + \overrightarrow {B’B} } \right).\overrightarrow {(D’C’} + \overrightarrow {C’C} ) = 2a.2a = 4{a^2}\)
\(\overrightarrow {D’A} .\overrightarrow {BC} = \left( {\overrightarrow {D’A’} + \overrightarrow {A’A} } \right).\overrightarrow {BC} = 2a.a = 2{a^2}\)
b,Góc \(\left( {\overrightarrow {A’D} ,\overrightarrow {B’C’} } \right)\)
Ta có: B’C’//A’D’