Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}), B({x_B};{y_B};{z_B})\) Biểu diễn mỗi vecto \(\ {OA}, \ {OB} \) theo các vecto \(\ i...

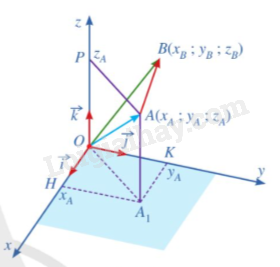
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\)

a.Biểu diễn mỗi vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \) và \(\overrightarrow k \)

b. Tìm liên hệ giữa \(\overrightarrow {AB} \) và \(({x_B} - {x_A}).\vec i + ({y_B} - {y_A}).\vec j + ({z_B} - {z_A}).\vec k\)

c. Từ đó, tìm tọa độ vecto \(\overrightarrow {AB} \)

Sử dụng lý thuyết tọa độ của vecto trong không gian

a) \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {OP} = \overrightarrow {OH} + \overrightarrow {OK} = {x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k \)

Tương tự, ta có: \(\overrightarrow {OB} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k \)

b) Ta có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k - ({x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k ) = ({x_B} - {x_A}).\overrightarrow i + ({y_B} - {y_A}).\overrightarrow j + ({z_B} - {z_A}).\overrightarrow k \)

c)Tọa độ vecto \(\overrightarrow {AB} ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)