Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 15
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;1} \right]\) và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:
a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất
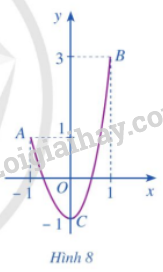

a) Điểm B là điểm thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm C là điểm thuộc đồ thị hàm số có tung độ nhỏ nhất
Advertisements (Quảng cáo)
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 16
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left( x \right) = \sqrt {9 - {x^2}} \) trên đoạn \(\left[ { - 3;3} \right]\).

Đánh giá dựa vào điều kiện xác định của x.

Ta có: \(x \in \left[ { - 3;3} \right] \Rightarrow 0 \le {x^2} \le 9 \Rightarrow 0 \le 9 - {x^2} \le 9 \Rightarrow 0 \le \sqrt {9 - {x^2}} \le 3\).
Vậy \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 3 \Leftrightarrow x = 0\\\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 0 \Leftrightarrow x = \pm 3\end{array} \right.\).
