Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 21
Xét hàm số \(y = f\left( x \right) = \frac{{26x + 10}}{{x + 5}}\) với \(x \in [0; + \infty )\) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
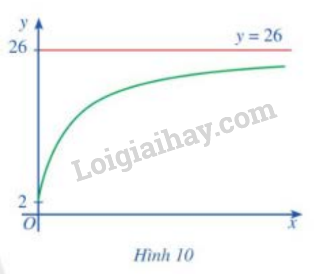
Quan sát đồ thị
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 26\)
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 22
Tìm tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 2}}{{x + 1}}\).
Đường thẳng \(y = {y_o}\) được gọi là đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_o}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_o}\).
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = 3\\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\end{array} \right.\).
Vậy đường thẳng \(y = 3\) là tiệm cận ngang của đồ thị hàm số đã cho